Innhold

• Trinn
• Metode 1 av 3: Hvordan løse en kubisk ligning uten et konstant begrep
• Metode 2 av 3: Hvordan finne hele røtter ved hjelp av multiplikatorer
• Metode 3 av 3: Hvordan løse en ligning ved hjelp av diskriminanten

I en kubisk ligning er den høyeste eksponenten 3, en slik ligning har 3 røtter (løsninger) og den har formen ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Noen kubiske ligninger er ikke så enkle å løse, men hvis du bruker riktig metode (med god teoretisk bakgrunn), kan du finne røttene til selv den mest komplekse kubiske ligningen - for dette kan du bruke formelen for å løse den kvadratiske ligningen, finne hele røtter, eller beregne diskriminanten.

Trinn

Metode 1 av 3: Hvordan løse en kubisk ligning uten et konstant begrep

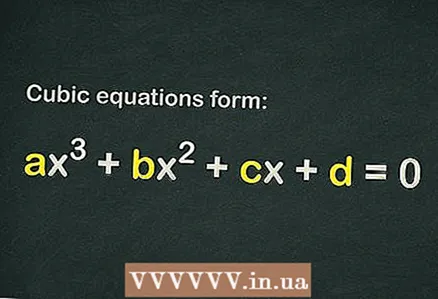1. 1 Finn ut om det er en ledig term i kubikkligningen d{ displaystyle d}. Den kubiske ligningen har formen ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... For at en ligning skal regnes som kubikk, er det tilstrekkelig at bare begrepet ${ displaystyle x ^ {3}}$ (det vil si at det kanskje ikke er andre medlemmer i det hele tatt).
   • Hvis ligningen har et fritt begrep ${ displaystyle d}$, bruk en annen metode.
   • Hvis i ligningen ${ displaystyle a = 0}$, det er ikke kubikk.
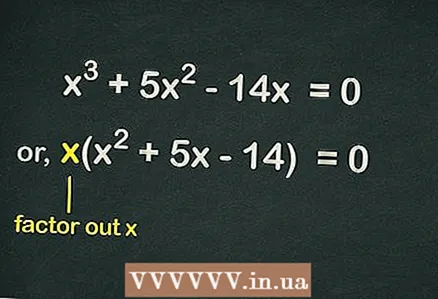2. 2 Ta ut av brakettene x{ displaystyle x}. Siden det ikke er noe fritt begrep i ligningen, inkluderer hvert begrep i ligningen variabelen ${ displaystyle x}$... Dette betyr at en ${ displaystyle x}$ kan utelukkes fra parenteser for å forenkle ligningen. Dermed vil ligningen skrives slik: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • For eksempel gitt en kubikkligning ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Ta ut ${ displaystyle x}$ parenteser og få ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
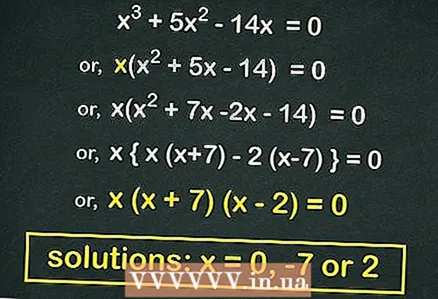3. 3 Faktor (produktet av to binomialer) den kvadratiske ligningen (hvis mulig). Mange kvadratiske ligninger av formen ${ displaystyle ax ^ {2} + bx + c = 0}$ kan faktoriseres. En slik ligning vil vise seg hvis vi tar ut ${ displaystyle x}$ utenfor brakettene. I vårt eksempel:
   • Ta ut av brakettene ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Faktor den kvadratiske ligningen: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Lik hver beholder til ${ displaystyle 0}$... Røttene til denne ligningen er ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Løs en kvadratisk ligning med en spesiell formel. Gjør dette hvis den kvadratiske ligningen ikke kan faktoriseres. For å finne to røtter av en ligning, verdiene til koeffisientene ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ erstatte i formelen ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • I vårt eksempel kan du erstatte verdiene til koeffisientene ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) i formelen:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Første rot:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Andre rot:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Bruk null og kvadratiske røtter som løsninger på kubikkligningen. Kvadratiske ligninger har to røtter, mens kubiske har tre. Du har allerede funnet to løsninger - dette er røttene til den kvadratiske ligningen. Hvis du setter "x" utenfor parentesene, vil den tredje løsningen være ${ displaystyle 0}$.
   • Hvis du tar "x" ut av parentesene, får du ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, det vil si to faktorer: ${ displaystyle x}$ og en kvadratisk ligning i parentes. Hvis noen av disse faktorene er ${ displaystyle 0}$, er hele ligningen også lik ${ displaystyle 0}$.
   • Således er to røtter av en kvadratisk ligning løsninger på en kubisk ligning. Den tredje løsningen er ${ displaystyle x = 0}$.

Metode 2 av 3: Hvordan finne hele røtter ved hjelp av multiplikatorer

1. 1 Sørg for at det er en ledig term i kubikkligningen d{ displaystyle d}. Hvis i en ligning av skjemaet ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ det er et gratis medlem ${ displaystyle d}$ (som ikke er lik null), vil det ikke fungere å sette "x" utenfor parentesene. I dette tilfellet, bruk metoden som er skissert i denne delen.
   • For eksempel gitt en kubikkligning ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... For å få null på høyre side av ligningen, legg til ${ displaystyle 6}$ til begge sider av ligningen.
   • Ligningen vil vise seg ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Som ${ displaystyle d = 6}$, kan metoden beskrevet i den første delen ikke brukes.
2. 2 Skriv ned faktorene til koeffisienten en{ displaystyle a} og et gratis medlem d{ displaystyle d}. Det vil si at du finner faktorene til tallet på ${ displaystyle x ^ {3}}$ og tall før likhetstegnet. Husk at faktorene til et tall er tallene som, når de multipliseres, gir det tallet.
   • For eksempel for å få nummeret 6, må du multiplisere ${ displaystyle 6 times 1}$ og ${ displaystyle 2 times 3}$... Så tallene 1, 2, 3, 6 er faktorer i tallet 6.
   • I vår ligning ${ displaystyle a = 2}$ og ${ displaystyle d = 6}$... Multiplikatorer 2 er 1 og 2... Multiplikatorer 6 er tallene 1, 2, 3 og 6.
3. 3 Del hver faktor en{ displaystyle a} for hver faktor d{ displaystyle d}. Som et resultat får du mange brøk og flere heltall; røttene til den kubiske ligningen vil være et av heltallene eller den negative verdien til et av heltallene.
   • I vårt eksempel, del faktorene ${ displaystyle a}$ (1 og 2) etter faktorer ${ displaystyle d}$ (1, 2, 3 og 6). Du vil få: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ og ${ displaystyle { frac {2} {3}}}$... Legg nå til negative verdier for de oppnådde brøkene og tallene i denne listen: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ og ${ displaystyle - { frac {2} {3}}}$... Hele røttene til den kubiske ligningen er noen tall fra denne listen.
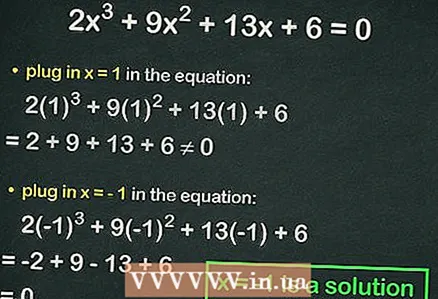4. 4 Plugg inn heltall i kubikkligningen. Hvis likheten er sann, er det substituerte tallet roten til ligningen. For eksempel, erstatt i ligningen ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, det vil si at likhet ikke blir observert. I dette tilfellet kobler du til det neste nummeret.
   • Erstatning ${ displaystyle -1}$: ${ displaystyle (-2) +9 +(- 13) +6}$ = 0. Dermed, ${ displaystyle -1}$ er hele roten av ligningen.
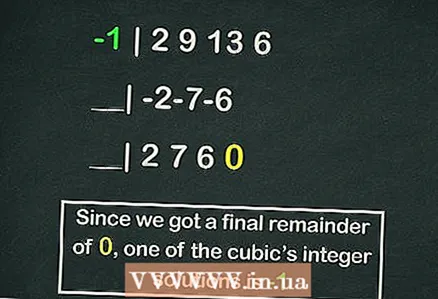5. 5 Bruk metoden for å dele polynom med Horners oppleggfor å finne røttene til ligningen raskere. Gjør dette hvis du ikke vil erstatte tall manuelt i ligningen. I Horners opplegg er heltall delt med verdiene til koeffisientene i ligningen ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ og ${ displaystyle d}$... Hvis tallene er jevnt delbare (det vil si resten ${ displaystyle 0}$), er et heltall roten til ligningen.
   • Horners opplegg fortjener en egen artikkel, men det følgende er et eksempel på beregning av en av røttene til vår kubiske ligning ved hjelp av denne ordningen:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Så resten er ${ displaystyle 0}$, men ${ displaystyle -1}$ er en av røttene til ligningen.

Metode 3 av 3: Hvordan løse en ligning ved hjelp av diskriminanten

1. 1 Skriv ned verdiene til koeffisientene i ligningen en{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} og d{ displaystyle d}. Vi anbefaler at du skriver ned verdiene til de angitte koeffisientene på forhånd for ikke å bli forvirret i fremtiden.
   • For eksempel gitt ligningen ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... Skrive ned ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ og ${ displaystyle d = -1}$... Husk det hvis før ${ displaystyle x}$ det er ikke noe tall, den tilsvarende koeffisienten eksisterer fortsatt og er lik ${ displaystyle 1}$.
2. 2 Beregn nulldiskriminanten ved å bruke en spesiell formel. For å løse en kubisk ligning ved hjelp av diskriminanten må du utføre en rekke vanskelige beregninger, men hvis du utfører alle trinnene riktig, blir denne metoden uunnværlig for å løse de mest komplekse kubiske ligningene. Første beregning ${ displaystyle Delta _ {0}}$ (null diskriminant) er den første verdien vi trenger; For å gjøre dette, erstatt de tilsvarende verdiene i formelen ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Diskriminanten er et tall som kjennetegner røttene til et polynom (for eksempel beregnes diskriminanten til en kvadratisk ligning med formelen ${ displaystyle b ^ {2} -4ac}$).
   • I vår ligning:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Beregn den første diskriminanten ved å bruke formelen Δ1=2b3−9enbc+27en2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Første diskriminerende ${ displaystyle Delta _ {1}}$ - dette er den andre viktige verdien; for å beregne det, koble de tilsvarende verdiene til den angitte formelen.
   • I vår ligning:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Regne ut:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Det vil si finne diskriminanten av kubikkligningen gjennom de oppnådde verdiene ${ displaystyle Delta _ {0}}$ og ${ displaystyle Delta _ {1}}$... Hvis diskriminanten av en kubisk ligning er positiv, har ligningen tre røtter; hvis diskriminanten er null, har ligningen en eller to røtter; hvis diskriminanten er negativ, har ligningen en rot.
   • En kubisk ligning har alltid minst en rot, siden grafen for denne ligningen skjærer X-aksen minst på et punkt.
   • I vår ligning ${ displaystyle Delta _ {0}}$ og ${ displaystyle Delta _ {1}}$ er like ${ displaystyle 0}$, slik at du enkelt kan beregne ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Dermed har ligningen vår en eller to røtter.

5. 5 Regne ut:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } høyre) div 2}}}$. ${ displaystyle C}$ - dette er den siste viktige mengden som blir funnet; det vil hjelpe deg med å beregne røttene til ligningen. Sett inn verdiene i den angitte formelen ${ displaystyle Delta _ {1}}$ og ${ displaystyle Delta _ {0}}$.
   • I vår ligning:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Finn tre røtter av ligningen. Gjør det med formelen ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, hvor ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, men n er lik 1, 2 eller 3... Sett inn de riktige verdiene i denne formelen - som et resultat får du tre røtter av ligningen.
   • Beregn verdien ved å bruke formelen på n = 1, 2 eller 3og sjekk deretter svaret. Hvis du får 0 når du sjekker svaret ditt, er denne verdien roten til ligningen.
   • I vårt eksempel, erstatt 1 i ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ og få 0, dvs 1 er en av røttene til ligningen.