Innhold

• Trinn
• Metode 1 av 2: Factoring
• Metode 2 av 2: Beregn Y
• Tips
• Advarsler

Hyperbola -asymptoter er rette linjer som går gjennom sentrum av hyperbolen. Hyperbola nærmer seg asymptotene, men krysser (eller berører) dem aldri. Det er to måter å finne likningene for asymptotene som vil hjelpe deg å forstå selve begrepet asymptoter.

Trinn

Metode 1 av 2: Factoring

1. 1 Skriv ned den kanoniske hyperbolligningen. La oss vurdere det enkleste eksemplet - en hyperbola, hvis sentrum ligger ved opprinnelsen. I dette tilfellet har den kanoniske hyperbola -ligningen formen: /_en - /_b = 1 (når grenene av hyperbola er rettet mot høyre eller venstre) eller /_b - /_en = 1 (når grenene til hyperbola er rettet opp eller ned). Husk at i denne ligningen er "x" og "y" variabler, og "a" og "b" er konstanter (det vil si tall).
   • Eksempel 1:/₉ - /₁₆ = 1
   • Noen lærere og læreboksforfattere bytter konstant "a" og "b". Studer derfor ligningen du har gitt for å forstå hva som er hva. Ikke bare husk ligningen - i dette tilfellet vil du ikke forstå noe hvis variabler og / eller konstanter er angitt med andre symboler.
2. 2 Sett den kanoniske ligningen til null (ikke en). Den nye ligningen beskriver begge asymptotene, men det tar litt innsats å få ligningen for hvert asymptot.
   • Eksempel 1:/₉ - /₁₆ = 0
3. 3 Faktor den nye ligningen. Faktor venstre side av ligningen. Husk hvordan du faktoriserer en kvadratisk ligning, og les videre.
   • Den siste ligningen (det vil si den faktoriserte ligningen) vil være (__ ± __) (__ ± __) = 0.
   • Når du multipliserer de første begrepene (inne i hvert par parenteser), bør du få begrepet /₉, så trekk ut kvadratroten fra dette medlemmet, og skriv resultatet i stedet for det første mellomrommet i hvert par parenteser: (/₃ ± __)(/₃ ± __) = 0
   • På samme måte trekker du ut kvadratroten til begrepet /₁₆, og skriv resultatet i stedet for det andre mellomrommet inne i hvert par parenteser: (/₃ ± /₄)(/₃ ± /₄) = 0
   • Du har funnet alle vilkårene i ligningen, så inne i ett par parenteser mellom begrepene skriver du et plusstegn, og inne i det andre - et minustegn, slik at når du multipliserer, blir de tilsvarende begrepene kansellert: (/₃ + /₄)(/₃ - /₄) = 0
4. 4 Sett hvert binomial (det vil si uttrykket i hvert par i parentes) til null og beregne "y". Dette vil finne to ligninger som beskriver hver asymptote.
   • Eksempel 1: Som (/₃ + /₄)(/₃ - /₄) = 0, da /₃ + /₄ = 0 og /₃ - /₄ = 0
   • Skriv om ligningen slik: /₃ + /₄ = 0 → /₄ = - /₃ → y = - /₃
   • Skriv om ligningen slik: /₃ - /₄ = 0 → - /₄ = - /₃ → y = /₃
5. 5 Utfør de beskrevne handlingene med en hyperbola hvis ligning er forskjellig fra den kanoniske. I det forrige trinnet fant du likningene for asymptotene til hyperbola sentrert ved opprinnelsen. Hvis midten av hyperbola er på et punkt med koordinater (h, k), beskrives det med følgende ligning: /_en - /_b = 1 eller /_b - /_en = 1. Denne ligningen kan også faktoriseres. Men i dette tilfellet må du ikke berøre binomialene (x - h) og (y - k) før du kommer til det siste trinnet.
   • Eksempel 2: /₄ - /₂₅ = 1
   • Sett denne ligningen til 0 og faktor den:
   • (/₂ + /₅)(/₂ - /₅) = 0
   • Lik hvert binomium (det vil si uttrykket inne i hvert par parenteser) til null og beregne "y" for å finne ligningene for asymptotene:
   • /₂ + /₅ = 0 → y = - /₂x + /₂
   • (/₂ - /₅) = 0 → y = /₂x - /₂

Metode 2 av 2: Beregn Y

1. 1 Isolere y -termen på venstre side av hyperbola -ligningen. Bruk denne metoden når hyperbola -ligningen er i kvadratisk form. Selv om det gis en kanonisk hyperbolligning, vil denne metoden gi en bedre forståelse av begrepet asymptoter. Isoler y eller (y - k) på venstre side av ligningen.
   • Eksempel 3:/₁₆ - /₄ = 1
   • Legg x til begge sider av ligningen, og multipliser deretter begge sider med 16:
   • (y + 2) = 16 (1 + /₄)
   • Forenkle den resulterende ligningen:
   • (y + 2) = 16 + 4 (x + 3)
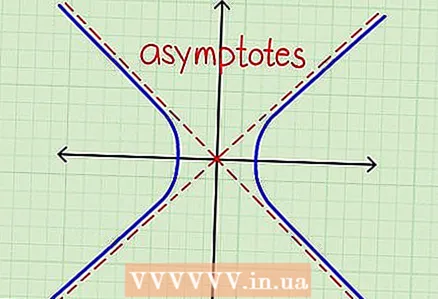
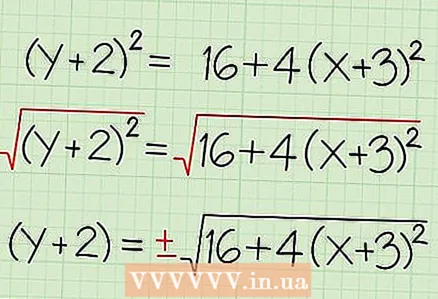2. 2 Ta kvadratroten på hver side av ligningen. Imidlertid må du ikke forenkle høyre side av ligningen for mye, siden når du trekker ut kvadratroten, får du to resultater -positive og negative (for eksempel -2 * -2 = 4, så √4 = 2 og √4 = -2). For å vise begge resultatene, bruk symbolet ±.
   • √ ((y + 2)) = √ (16 + 4 (x + 3))
   • (y + 2) = ± √ (16 + 4 (x + 3))
3. 3 Forstå begrepet asymptoter. Gjør dette før du går videre til neste trinn. En asymptote er en rett linje, som hyperbola nærmer seg med økende verdier av "x".Hyperbola vil aldri krysse asymptoten, men med økende "x" vil hyperbolen nærme seg asymptoten i uendelig liten avstand.
4. 4 Transformer ligningen for å ta høyde for store x -verdier. Som regel, når du arbeider med likningene for asymptoter, blir bare store verdier av "x" tatt i betraktning (det vil si de verdiene som har en tendens til uendelig). Derfor kan visse konstanter negligeres i ligningen, siden deres bidrag er lite sammenlignet med "x". For eksempel, hvis variabelen "x" er lik flere milliarder, vil addisjonen av tallet (konstant) 3 ha en ubetydelig effekt på verdien av "x".
   • I ligningen (y + 2) = ± √ (16 + 4 (x + 3)) ettersom “x” har en tendens til uendelig, kan konstanten 16 ignoreres.
   • For store verdier av "x" (y + 2) ≈ ± √ (4 (x + 3))
5. 5 Beregn y for å finne likningene for asymptotene. Ved å kvitte seg med konstantene kan du forenkle det radikale uttrykket. Husk at du må skrive to ligninger i svaret ditt - en med et plusstegn og den andre med et minustegn.
   • y + 2 = ± √ (4 (x + 3) ^ 2)
   • y + 2 = ± 2 (x + 3)
   • y + 2 = 2x + 6 og y + 2 = -2x - 6
   • y = 2x + 4ogy = -2x - 8

Tips

• Husk at ligningen for hyperbola og likningene for dets asymptoter alltid inkluderer konstanter (konstanter).
• En likesidet hyperbola er en hyperbola i ligningen som a = b = c (konstant).
• Hvis du får en likesidet hyperbola -ligning, må du først konvertere den til kanonisk form og deretter finne ligningene for asymptotene.

Advarsler

• Husk at svaret ikke alltid er skrevet i kanonisk form.