Innhold

• Fremgangsmåte
• Råd

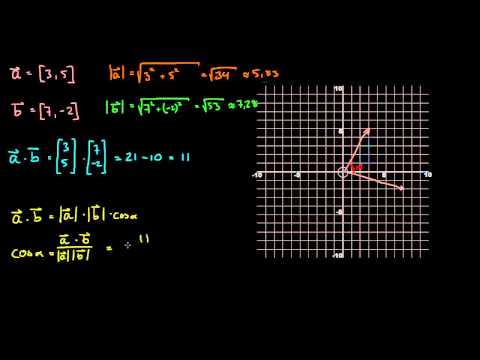
Hvis du er matematiker eller grafisk programmerer, må du sannsynligvis finne vinkelen mellom to gitte vektorer. I denne artikkelen viser wikiHow deg hvordan du gjør nettopp det.

Fremgangsmåte

Del 1 av 2: Finn vinkelen mellom to vektorer

1. 

   Vector definisjon. Skriv ned all informasjonen om de to vektorene du har. Anta at du bare har de angitte parametrene for deres dimensjonale koordinater (også kalt komponenter). Hvis du allerede vet lengden (størrelsen) på en vektor, kan du hoppe over noen av trinnene nedenfor.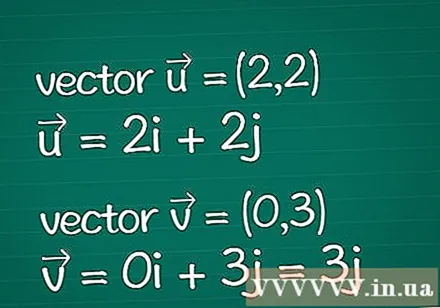
   • Eksempel: To-dimensjonal vektor = (2,2) og to-dimensjonal vektor = (0,3). De kan også skrives som = 2Jeg + 2j og = 0Jeg + 3j = 3j.
   • Selv om todimensjonale vektorer brukes i eksemplet i denne artikkelen, kan følgende instruksjoner gjelde for vektorer med et hvilket som helst antall dimensjoner.

2. 

   
   
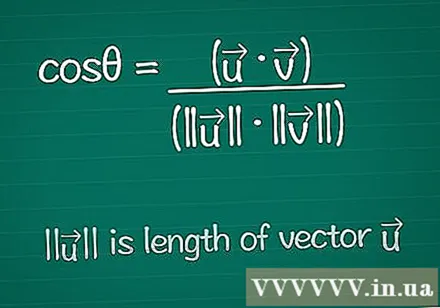
   Skriv ned cosinusformelen. For å finne vinkelen θ mellom to vektorer, begynner vi med formelen for å finne cosinus for den vinkelen. Du kan lære om denne formelen nedenfor, eller bare skrive den ned slik:
   • cosθ = (•) / (|||| ||||)
   • |||| betyr "lengden på vektoren".
   • • er skalarproduktet til de to vektorene - dette vil bli forklart nedenfor.

3. 

   
   
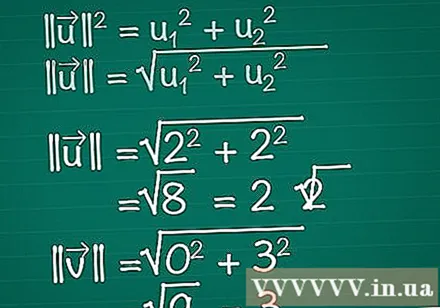
   Beregn lengden på hver vektor. Tenk deg at en høyre trekant består av x, y-komponentene i vektoren og selve vektoren. Vektoren danner hypotenusen til trekanten, så for å finne lengden bruker vi den pythagoriske teoremet. Faktisk kan denne formelen lett utvides til en vektor med et hvilket som helst antall dimensjoner.
   • || u || = u₁ + u₂. Hvis en vektor har mer enn to elementer, trenger du bare å fortsette å legge til + u₃ + u₄ +...
   • Derfor, for en todimensjonal vektor, || u || = √ (u₁ + u₂).
   • I dette eksemplet |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
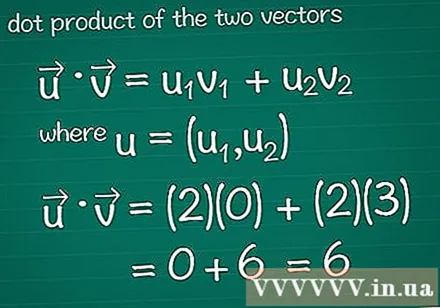
   Beregn skalarproduktet til to vektorer. Kanskje du har lært metoden for vektormultiplikasjon, også kjent som skalar dette. For å beregne det skalære produktet i forhold til sammensetningen, multipliser du ingrediensene i hver retning sammen, og legg deretter sammen hele resultatet.
   • For grafikkprogrammet, se Tips før du leser videre.
   • I matte • = u₁v₁ + u₂v₂, hvor, u = (u₁, u₂). Hvis vektoren har mer enn to elementer, er det bare å legge til + u₃v₃ + u₄v₄...
   • I dette eksemplet er • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dette er det skalære produktet til vektoren og vektoren.

5. 

   Sett resultatene i formelen. Husk at cosθ = (•) / (|||| || ||). Nå vet vi både det skalære produktet og lengden på hver vektor. Skriv disse inn i formelen for å beregne vinkelens cosinus.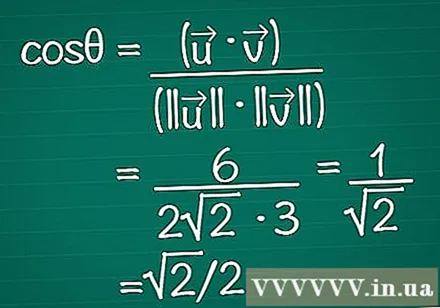
   • I vårt eksempel er cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Finn vinkelen basert på dens cosinus. Du kan bruke arccos eller cos-funksjonen i en kalkulator for å finne θ fra en kjent cos-verdi. Med noen resultater kan du finne vinkelen basert på enhetssirkelen.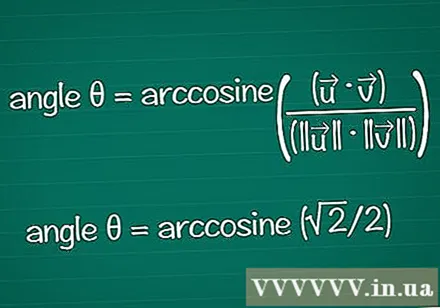
   • I eksemplet er cosθ = √2 / 2. Angi "arccos (√2 ​​/ 2)" i kalkulatoren for å finne vinkelen. Eller du kan finne vinkelen θ på enhetssirkelen, i posisjon cosθ = √2 / 2. Det er sant for θ = /₄ eller 45º.
   • Når du kombinerer alt, er den endelige formelen: vinkel θ = arkkosin ((•) / (|||| || ||))
   annonse

Del 2 av 2: Bestemmelse av vinkelformel

1. 

   Forstå formålet med formelen. Denne formelen ble ikke hentet fra eksisterende regler. I stedet er den dannet som definisjonen av skalarproduktet og vinkelen mellom de to vektorene. Likevel var det ikke en vilkårlig avgjørelse. Når vi går tilbake til grunnleggende geometri, kan vi forstå hvorfor denne formelen gir intuitive og nyttige definisjoner.
   • Eksemplene nedenfor bruker todimensjonale vektorer fordi de er lettest å forstå og enkleste. Tredimensjonale eller flere vektorer har egenskaper definert av nesten like generelle formler.

2. 

   Gjennomgå Cosines teorem. Tenk på en vanlig trekant med vinkel θ mellom sidene a og b, motsatt side c. Cosines teorem sier at c = a + b -2abcos(θ). Dette resultatet er ganske enkelt hentet fra grunnleggende geometri.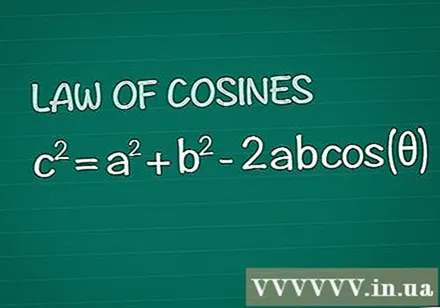

3. 

   Koble to vektorer og danner en trekant. Tegn et par todimensjonale vektorer på papir, vektorer og vektorer, med θ som vinkelen mellom dem. Tegn en tredje vektor mellom disse to for å lage en trekant. Tegn med andre ord en vektor slik at + =. Vector = -.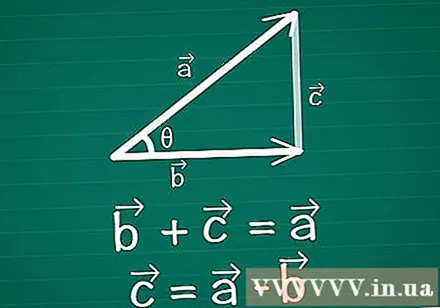

4. 

   Skriv Cosine-setningen for denne trekanten. Erstatt sidelengden av vår "vektortrekant" i Cosine-setningen:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Skriv om med skalarprodukt. Husk at et skalarprodukt er bildet av en vektor på den andre. Det skalære produktet til en vektor med seg selv krever ingen projeksjon, for her er det ingen forskjell i retning. Det betyr • = || a ||. Ved å bruke dette omskriver vi ligningen:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Omskrevet den samme formelen. Utvid venstre side av formelen, og forenkle for å få formelen brukt til å finne vinkler.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   annonse

Råd

• For å endre verdier og løse problemet raskt, bruk denne formelen for et par todimensjonale vektorer: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Hvis du jobber med datagrafikkprogramvare, er sjansen stor for at du bare trenger å bekymre deg for vektordimensjonene uten å bekymre deg for lengden. Bruk følgende trinn for å forkorte en ligning og øke hastigheten på programmet:
  • Normaliser hver vektor slik at de er lik 1. For å gjøre dette, del hver av vektorkomponentene med lengden.
  • Få det normaliserte produktet av skalaren i stedet for den opprinnelige vektoren.
  • Siden lengden er 1, kan vi ekskludere lengdeelementene fra ligningen. Til slutt er vinkellikningen oppnådd arccos (•).
• Basert på cosinusformelen kan vi raskt avgjøre om vinkelen er spiss eller stump. Start med cosθ = (•) / (|||| ||||):
  • Venstre og høyre side av ligningen må ha samme tegn (positiv eller negativ).
  • Siden lengden alltid er positiv, må cosθ ha samme tegn som skalarproduktet.
  • Derfor, hvis produktet er positivt, er cosθ også positivt. Vi er i den første kvadranten av enhetssirkelen, med θ <π / 2 eller 90º. Vinkelen er skarp.
  • Hvis skalarproduktet er negativt, er cosθ negativt. Vi er i den andre kvadranten av enhetssirkelen, med π / 2 <θ ≤ π eller 90º <θ ≤ 180º. Det er fengselshjørnet.