Innhold

• Å trå
• Metode 1 av 2: Test den algebraisk funksjonen
• Tips
• Advarsel

En måte å klassifisere funksjoner på er enten som "jevn", "merkelig" eller som ingen av dem. Disse begrepene refererer til repetisjon eller symmetri av funksjonen. Den beste måten å finne ut av dette er å manipulere funksjonen algebraisk. Du kan også studere grafen til funksjonen og se etter symmetri. Når du vet hvordan du skal klassifisere funksjoner, kan du også forutsi utseendet til visse kombinasjoner av funksjoner.

Å trå

Metode 1 av 2: Test den algebraisk funksjonen

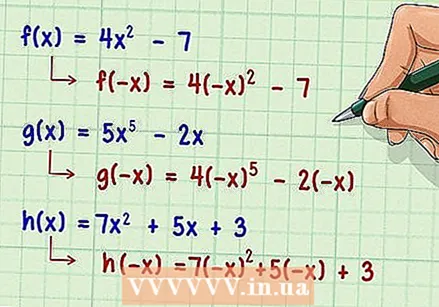1. Vis omvendte variabler. I algebra er det inverse av en variabel negativ. Dette er sant eller variabelen til funksjonen nå ${ displaystyle x}$Erstatt hver variabel i funksjonen med dens inverse. Ikke endre den opprinnelige funksjonen unntatt tegnet. For eksempel:
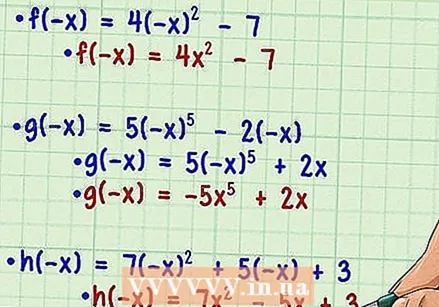   • ${ displaystyle f (x) = 4x ^ {2} -7}$Forenkle den nye funksjonen. På dette punktet trenger du ikke å bekymre deg for å løse funksjonen for en gitt numerisk verdi. Du forenkler bare variablene for å sammenligne den nye funksjonen, f (-x), med den opprinnelige funksjonen, f (x). Husk grunnleggende regler for eksponenter som sier at en negativ base til en jevn kraft vil være positiv, mens en negativ base vil være negativ til en merkelig kraft.
     • ${ displaystyle f (-x) = 4 (-x) ^ {2} -7}$Sammenlign de to funksjonene. For hvert eksempel du prøver, sammenlign den forenklede versjonen av f (-x) med den opprinnelige f (x). Plasser vilkårene side om side for enkel sammenligning, og sammenlign tegn på alle vilkår.
       • Hvis de to resultatene er de samme, er f (x) = f (-x), og den opprinnelige funksjonen er jevn. Et eksempel er:
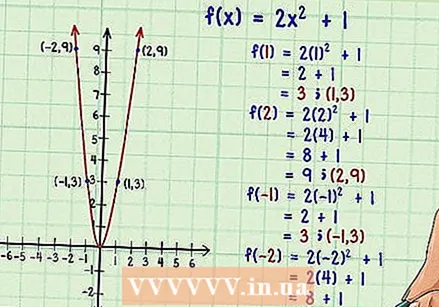         • ${ displaystyle f (x) = 4x ^ {2} -7}$Graf funksjonen. Bruk grafpapir eller en grafkalkulator for å tegne funksjonen. Velg forskjellige numeriske verdier for det 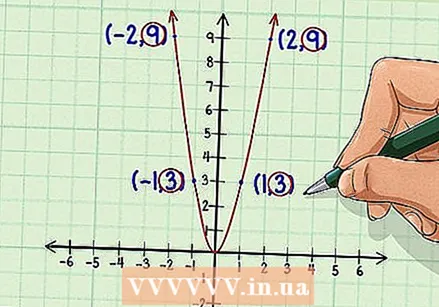${ displaystyle x}$Merk symmetri langs y-aksen. Når du ser på en funksjon, vil symmetri antyde et speilbilde. Hvis du ser at den delen av grafen på høyre (positive) side av y-aksen samsvarer med den delen av grafen på venstre (negative) side av y-aksen, er grafen symmetrisk rundt y-aksen. Aske. Hvis en funksjon er symmetrisk rundt y-aksen, er funksjonen jevn.
           • Du kan teste for symmetri ved å velge individuelle punkter.Hvis y-verdien til en hvilken som helst x-verdi er den samme som y-verdien til -x, er funksjonen jevn. Punktene valgt ovenfor for å plotte 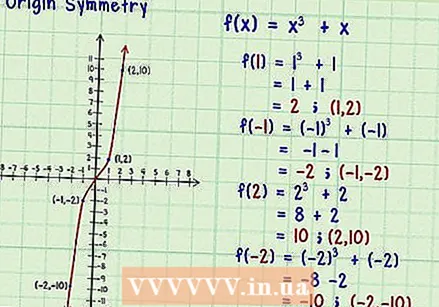${ displaystyle f (x) = 2x ^ {2} +1}$Test for symmetri fra opprinnelsen. Opprinnelsen er det sentrale punktet (0,0). Opprinnelsessymmetri betyr at et positivt resultat for en valgt x-verdi vil tilsvare et negativt resultat for -x, og omvendt. Odd-funksjoner viser opprinnelsessymmetri.
             • Hvis du velger et par testverdier for x og deres inverse korresponderende verdier for -x, bør du få inverse resultater. Tenk på funksjonen 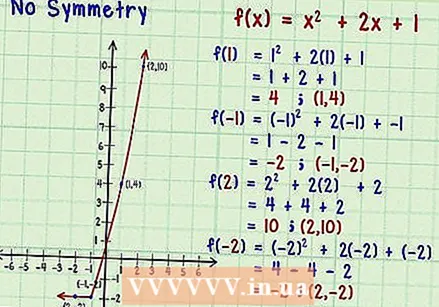${ displaystyle f (x) = x ^ {3} + x}$Se om det ikke er symmetri. Det siste eksemplet er en funksjon uten symmetri på begge sider. Hvis du ser på grafen, vil du se at det ikke er et speilbilde på verken y-aksen eller rundt opprinnelsen. Sjekk ut funksjonen ${ displaystyle f (x) = x ^ {2} + 2x + 1}$.
               • Velg noen få verdier for x og -x, som følger:
                 • ${ displaystyle f (1) = 1 ^ {2} +2 (1) + 1 = 1 + 2 + 1 = 4}$. Poenget med å plotte er (1,4).
                 • ${ displaystyle f (-1) = (- 1) ^ {2} +2 (-1) + (- 1) = 1-2-1 = -2}$. Poenget å plotte er (-1, -2).
                 • ${ displaystyle f (2) = 2 ^ {2} +2 (2) + 2 = 4 + 4 + 2 = 10}$. Poenget å plotte er (2,10).
                 • ${ displaystyle f (-2) = (- 2) ^ {2} +2 (-2) + (- 2) = 4-4-2 = -2}$. Poenget å plotte er (2, -2).
               • Dette gir deg allerede nok poeng til å legge merke til at det ikke er noen symmetri. Y-verdiene for motsatte par x-verdier er ikke de samme, og de er heller ikke motsatte av hverandre. Denne funksjonen er verken jevn eller merkelig.
               • Du kan se at denne funksjonen, ${ displaystyle f (x) = x ^ {2} + 2x + 1}$, kan skrives om som ${ displaystyle f (x) = (x + 1) ^ {2}}$. Skrevet i denne formen ser det ut som om det er en jevn funksjon fordi det bare er en eksponent, som er et partall. Dette eksemplet illustrerer imidlertid at du ikke kan avgjøre om en funksjon er jevn eller merkelig når den er lukket i parentes. Du må utdype funksjonen i separate vilkår og deretter undersøke eksponentene.

Tips

• Hvis alle former for en variabel i funksjonen har jevne eksponenter, er funksjonen jevn. Hvis alle eksponentene er rare, er funksjonen underlig generelt.

Advarsel

• Denne artikkelen gjelder bare funksjoner med to variabler, som kan tegnes i et todimensjonalt koordinatsystem.