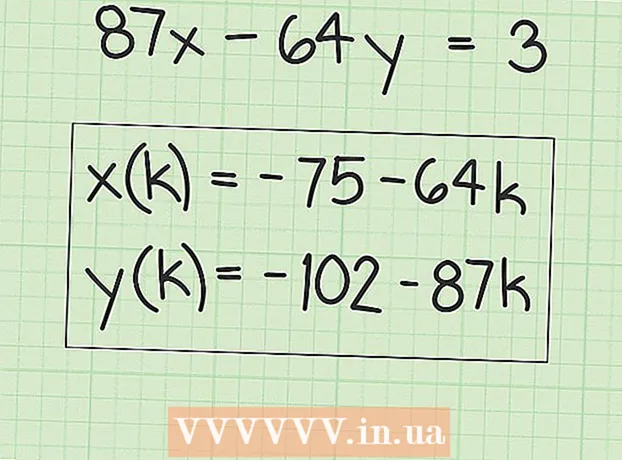
Innhold

• Trinn
• Del 1 av 4: Hvordan skrive en ligning
• Del 2 av 4: Hvordan skrive Euklids algoritme
• Del 3 av 4: Hvordan finne en løsning ved hjelp av Euclids algoritme
• Del 4 av 4: Finn uendelige andre løsninger

For å løse en lineær Diophantine -ligning må du finne verdiene til variablene "x" og "y", som er heltall. En heltallsløsning er mer kompleks enn vanlig og krever et bestemt sett med handlinger. Først må du beregne den største fellesdeleren (GCD) for koeffisientene, og deretter finne en løsning. Når du har funnet en heltall løsning til en lineær ligning, kan du bruke et enkelt mønster for å finne et uendelig antall andre løsninger.

Trinn

Del 1 av 4: Hvordan skrive en ligning

1. 1 Skriv ligningen ned i standardform. En lineær ligning er en ligning der eksponentene til variablene ikke overstiger 1. For å løse en slik lineær ligning, skriv den først i standardform. Standardformen for en lineær ligning ser slik ut: ${ displaystyle Ax + By = C}$, hvor ${ displaystyle A, B}$ og ${ displaystyle C}$ - hele tall.
   • Hvis ligningen er gitt i en annen form, må du bringe den til standardform ved hjelp av grunnleggende algebraiske operasjoner. For eksempel gitt ligningen ${ displaystyle 23x + 4y -7x = -3y + 15}$... Gi lignende uttrykk og skriv ligningen slik: ${ displaystyle 16x + 7y = 15}$.
2. 2 Forenkle ligningen (hvis mulig). Når du skriver ligningen i standardform, se på koeffisientene ${ displaystyle A, B}$ og ${ displaystyle C}$... Hvis disse oddsen har en GCD, deler du alle tre oddsen med den. Løsningen på en slik forenklet ligning vil også være løsningen på den opprinnelige ligningen.
   • For eksempel, hvis alle tre koeffisientene er like, del dem med minst 2. For eksempel:
     • ${ displaystyle 42x + 36y = 48}$ (alle medlemmer er delbare med 2)
     • ${ displaystyle 21x + 18y = 24}$ (nå er alle medlemmer delbare med 3)
     • ${ displaystyle 7x + 6y = 8}$ (denne ligningen kan ikke lenger forenkles)
3. 3 Sjekk om ligningen kan løses. I noen tilfeller kan du umiddelbart opplyse at ligningen ikke har noen løsninger. Hvis koeffisienten "C" ikke er delelig med GCD for koeffisientene "A" og "B", har ligningen ingen løsninger.
   • For eksempel hvis begge koeffisientene ${ displaystyle A}$ og ${ displaystyle B}$ er jevne, så er koeffisienten ${ displaystyle C}$ må være jevn. Men hvis ${ displaystyle C}$ merkelig, så er det ingen løsning.
     • Ligningen ${ displaystyle 2x + 4y = 21}$ ingen heltallsløsninger.
     • Ligningen ${ displaystyle 5x + 10y = 17}$ det er ingen heltallløsninger siden venstre side av ligningen er delelig med 5 og høyre side ikke.

Del 2 av 4: Hvordan skrive Euklids algoritme

1. 1 Forstå Euclids algoritme. Det er en serie gjentatte divisjoner der den forrige resten ble brukt som den neste deleren. Den siste deleren som deler tallene integrert er den største fellesdeleren (GCD) av de to tallene.
   • La oss for eksempel finne GCD av tallene 272 og 36 ved hjelp av Euclids algoritme:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Del det større tallet (272) med det mindre (36) og vær oppmerksom på resten (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - del den forrige deleren (36) med den forrige resten (20). Legg merke til den nye resten (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - del den forrige deleren (20) med den forrige resten (16). Legg merke til den nye resten (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Del den forrige deleren (16) med den forrige resten (4). Siden resten er 0, kan vi si at 4 er GCD for de to opprinnelige tallene 272 og 36.
2. 2 Bruk Euclids algoritme på koeffisientene "A" og "B". Når du skriver den lineære ligningen i standardform, bestem koeffisientene "A" og "B" og bruk deretter Euklids algoritme til dem for å finne GCD. For eksempel gitt en lineær ligning ${ displaystyle 87x-64y = 3}$.
   • Her er Euklids algoritme for koeffisientene A = 87 og B = 64:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Finn den største fellesfaktoren (GCD). Siden den siste divisoren var 1, er GCD 87 og 64 1. Dermed er 87 og 64 primtall i forhold til hverandre.
4. 4 Analyser resultatet. Når du finner gcd -koeffisientene ${ displaystyle A}$ og ${ displaystyle B}$, sammenligne det med koeffisienten ${ displaystyle C}$ den opprinnelige ligningen. Hvis ${ displaystyle C}$ delelig med gcd ${ displaystyle A}$ og ${ displaystyle B}$, ligningen har en heltall løsning; ellers har ligningen ingen løsninger.
   • For eksempel ligningen ${ displaystyle 87x-64y = 3}$ kan løses fordi 3 er delelig med 1 (gcd = 1).
   • Anta for eksempel GCD = 5. 3 er ikke jevnt delelig med 5, så denne ligningen har ingen heltallsløsninger.
   • Som vist nedenfor, hvis en ligning har én heltall løsning, har den også et uendelig antall andre heltall løsninger.

Del 3 av 4: Hvordan finne en løsning ved hjelp av Euclids algoritme

1. 1 Nummerer trinnene for å beregne GCD. For å finne løsningen på en lineær ligning, må du bruke den euklidiske algoritmen som grunnlag for substitusjons- og forenklingsprosessen.
   • Start med å nummerere trinnene for å beregne GCD. Beregningsprosessen ser slik ut:
     • ${ displaystyle { text {Step 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Trinn 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {Trinn 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Trinn 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Trinn 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Step 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Step 7}}: 2 = (2 * 1) +0}$
2. 2 Vær oppmerksom på det siste trinnet, der det er en rest. Skriv om ligningen for dette trinnet for å isolere resten.
   • I vårt eksempel er det siste trinnet med resten trinn 6. Resten er 1. Skriv om ligningen i trinn 6 som følger:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Isolere resten av forrige trinn. Denne prosessen er et trinn-for-trinn "gå opp". Hver gang vil du isolere resten i ligningen i forrige trinn.
   • Isolere resten av ligningen i trinn 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ eller ${ displaystyle 2 = 5-3}$
4. 4 Erstatt og forenkle. Legg merke til at ligningen i trinn 6 inneholder tallet 2, og i ligningen i trinn 5 er tallet 2 isolert. Så i stedet for "2" i ligningen i trinn 6, erstatt uttrykket i trinn 5:
   • ${ displaystyle 1 = 3-2}$ (ligning av trinn 6)
   • ${ displaystyle 1 = 3- (5-3)}$ (i stedet for 2 ble et uttrykk erstattet)
   • ${ displaystyle 1 = 3-5 + 3}$ (åpnet parentes)
   • ${ displaystyle 1 = 2 (3) -5}$ (forenklet)
5. 5 Gjenta substitusjons- og forenklingsprosessen. Gjenta den beskrevne prosessen, beveg deg gjennom den euklidiske algoritmen i motsatt rekkefølge. Hver gang du vil skrive ligningen fra forrige trinn og koble den til den siste ligningen du får.
   • Det siste trinnet vi så på var trinn 5. Så gå til trinn 4 og isoler resten i ligningen for det trinnet:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Erstatt dette uttrykket med "3" i den siste ligningen:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Fortsett med substitusjons- og forenklingsprosessen. Denne prosessen vil gjentas til du når det første trinnet i den euklidiske algoritmen. Målet med prosessen er å skrive ligningen med koeffisientene 87 og 64 i den opprinnelige ligningen som skal løses. I vårt eksempel:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (erstattet uttrykket fra trinn 3)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (erstattet uttrykket fra trinn 2)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (erstattet uttrykket fra trinn 1)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Omskrive den resulterende ligningen i samsvar med de opprinnelige koeffisientene. Når du går tilbake til det første trinnet i den euklidiske algoritmen, vil du se at den resulterende ligningen inneholder to koeffisienter av den opprinnelige ligningen. Skriv om ligningen slik at rekkefølgen på vilkårene samsvarer med koeffisientene til den opprinnelige ligningen.
   • I vårt eksempel, den opprinnelige ligningen ${ displaystyle 87x-64y = 3}$... Skriv derfor om den resulterende ligningen slik at koeffisientene bringes på linje.Vær spesielt oppmerksom på koeffisienten "64". I den opprinnelige ligningen er denne koeffisienten negativ, og i den euklidiske algoritmen er den positiv. Derfor må faktoren 34 gjøres negativ. Den siste ligningen vil bli skrevet slik:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Bruk riktig multiplikator for å finne en løsning. Legg merke til at i vårt eksempel er GCD = 1, så den endelige ligningen er 1. Men den opprinnelige ligningen (87x-64y) er 3. Derfor må alle termer i den endelige ligningen multipliseres med 3 for å få løsningen:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Skriv ned heltaleløsningen til ligningen. Tallene som multipliseres med koeffisientene til den opprinnelige ligningen er løsningene på denne ligningen.
   • I vårt eksempel skriver du løsningen som et par koordinater: ${ displaystyle (x, y) = ( - 75, -102)}$.

Del 4 av 4: Finn uendelige andre løsninger

1. 1 Forstå at det er uendelig mange løsninger. Hvis en lineær ligning har én heltall løsning, må den ha uendelig mange heltall løsninger. Her er et raskt bevis (i algebraisk form):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (hvis du legger til "B" til "x" og trekker "A" fra "y", endres ikke verdien til den opprinnelige ligningen)
2. 2 Registrer de opprinnelige x- og y -verdiene. Malen for å beregne de neste (uendelige) løsningene starter med den eneste løsningen du allerede har funnet.
   • I vårt eksempel er løsningen et par koordinater ${ displaystyle (x, y) = ( - 75, -102)}$.
3. 3 Legg til "B" -faktoren til "x" -verdien. Gjør dette for å finne den nye x -verdien.
   • I vårt eksempel er x = -75 og B = -64:
     • ${ displaystyle x = -75 + ( - 64) = - 139}$
   • Dermed er den nye verdien "x": x = -139.
4. 4 Trekk "A" -faktoren fra "y" -verdien. For at verdien til den opprinnelige ligningen ikke skal endres, må du trekke et annet tall fra "y" når du legger et tall til "x".
   • I vårt eksempel y = -102 og A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Dermed er den nye verdien for "y": y = -189.
   • Det nye paret koordinater vil bli skrevet slik: ${ displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Sjekk løsningen. For å bekrefte at det nye koordinatparet er en løsning på den opprinnelige ligningen, kobler du verdiene til ligningen.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Siden likestillingen er oppfylt, er avgjørelsen riktig.
6. 6 Skriv ned uttrykk for å finne mange løsninger. "X" -verdiene tilsvarer den opprinnelige løsningen pluss et multiplum av "B" -faktoren. Dette kan skrives som følgende uttrykk:
   • x (k) = x + k (B), hvor "x (k)" er settet med "x" -verdier og "x" er den opprinnelige (første) verdien av "x" som du fant.
     • I vårt eksempel:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), der y (k) er settet med y-verdier og y er den opprinnelige (første) y-verdien du fant.
     • I vårt eksempel:
     • ${ displaystyle y (k) = - 102-87k}$