Forfatter:
Eric Farmer
Opprettelsesdato:
7 Mars 2021
Oppdater Dato:
1 Juli 2024

Innhold
- Trinn
- Metode 1 av 4: Beregning av korrelasjonskoeffisienten manuelt
- Metode 2 av 4: Bruke online kalkulatorer til å beregne korrelasjonskoeffisienten
- Metode 3 av 4: Bruke en grafisk kalkulator
- Metode 4 av 4: Forklaring av grunnleggende begreper
- Tips
- Advarsler
Korrelasjonskoeffisienten (eller lineær korrelasjonskoeffisient) er betegnet som "r" (i sjeldne tilfeller som "ρ") og karakteriserer den lineære korrelasjonen (det vil si forholdet som er gitt av en verdi og retning) av to eller flere variabler. Verdien av koeffisienten ligger mellom -1 og +1, det vil si at korrelasjonen kan være både positiv og negativ. Hvis korrelasjonskoeffisienten er -1, er det en perfekt negativ korrelasjon; hvis korrelasjonskoeffisienten er +1, er det en perfekt positiv korrelasjon. Ellers er det en positiv korrelasjon mellom de to variablene, en negativ korrelasjon eller ingen korrelasjon. Korrelasjonskoeffisienten kan beregnes manuelt, med gratis online kalkulatorer, eller med en god grafisk kalkulator.
Trinn
Metode 1 av 4: Beregning av korrelasjonskoeffisienten manuelt
 1 Samle data. Før du begynner å beregne korrelasjonskoeffisienten, studer disse tallparene. Bedre å skrive dem ned i en tabell som kan ordnes vertikalt eller horisontalt. Merk hver rad eller kolonne med "x" og "y".
1 Samle data. Før du begynner å beregne korrelasjonskoeffisienten, studer disse tallparene. Bedre å skrive dem ned i en tabell som kan ordnes vertikalt eller horisontalt. Merk hver rad eller kolonne med "x" og "y". - For eksempel gitt fire par verdier (tall) til variablene "x" og "y". Du kan lage følgende tabell:
- x || y
- 1 || 1
- 2 || 3
- 4 || 5
- 5 || 7
- For eksempel gitt fire par verdier (tall) til variablene "x" og "y". Du kan lage følgende tabell:
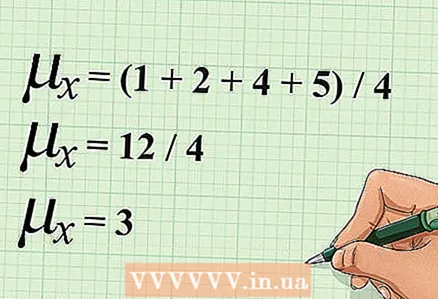 2 Beregn det aritmetiske gjennomsnittet "x". For å gjøre dette, legg til alle x -verdiene, og divider deretter resultatet med antall verdier.
2 Beregn det aritmetiske gjennomsnittet "x". For å gjøre dette, legg til alle x -verdiene, og divider deretter resultatet med antall verdier. - I vårt eksempel er det fire verdier for variabelen "x". For å beregne det aritmetiske gjennomsnittet "x", legg til disse verdiene, og del deretter summen med 4. Beregningene er skrevet som følger:
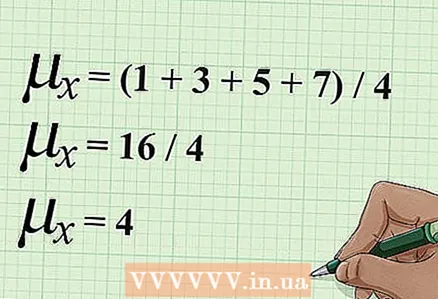 3 Finn det aritmetiske gjennomsnittet "y". For å gjøre dette, følg de samme trinnene, det vil si å legge sammen alle y -verdiene, og deretter dele summen med antall verdier.
3 Finn det aritmetiske gjennomsnittet "y". For å gjøre dette, følg de samme trinnene, det vil si å legge sammen alle y -verdiene, og deretter dele summen med antall verdier. - I vårt eksempel er fire verdier av variabelen "y" gitt. Legg til disse verdiene, og del deretter summen med 4. Beregningene skrives som følger:
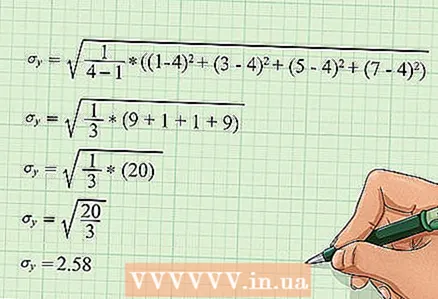
 4 Beregn standardavviket "x". Etter å ha beregnet middelene til "x" og "y", finner du standardavvikene til disse variablene. Standardavviket beregnes ved hjelp av følgende formel:
4 Beregn standardavviket "x". Etter å ha beregnet middelene til "x" og "y", finner du standardavvikene til disse variablene. Standardavviket beregnes ved hjelp av følgende formel: - I vårt eksempel vil beregningene bli skrevet slik:
 5 Beregn standardavviket "y". Følg trinnene som er beskrevet i forrige trinn. Bruk samme formel, men sett inn y -verdiene.
5 Beregn standardavviket "y". Følg trinnene som er beskrevet i forrige trinn. Bruk samme formel, men sett inn y -verdiene. - I vårt eksempel vil beregningene skrives slik:
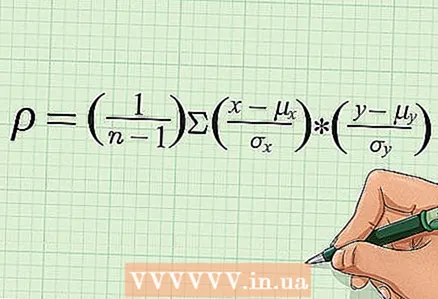 6 Skriv ned grunnformelen for å beregne korrelasjonskoeffisienten. Denne formelen inkluderer middel, standardavvik og antall (n) par med tall for begge variablene. Korrelasjonskoeffisienten er betegnet som "r" (i sjeldne tilfeller som "ρ"). Denne artikkelen bruker en formel for å beregne Pearson -korrelasjonskoeffisienten.
6 Skriv ned grunnformelen for å beregne korrelasjonskoeffisienten. Denne formelen inkluderer middel, standardavvik og antall (n) par med tall for begge variablene. Korrelasjonskoeffisienten er betegnet som "r" (i sjeldne tilfeller som "ρ"). Denne artikkelen bruker en formel for å beregne Pearson -korrelasjonskoeffisienten. - Her og i andre kilder kan mengder betegnes på forskjellige måter. Noen formler inneholder for eksempel “ρ” og “σ”, mens andre inneholder “r” og “s”. Noen lærebøker gir forskjellige formler, men de er matematiske motstykker til formelen ovenfor.
 7 Beregn korrelasjonskoeffisienten. Du har beregnet gjennomsnitt og standardavvik for begge variablene, så du kan bruke formelen til å beregne korrelasjonskoeffisienten. Husk at "n" er antall verdipar for begge variablene. Andre verdier er beregnet tidligere.
7 Beregn korrelasjonskoeffisienten. Du har beregnet gjennomsnitt og standardavvik for begge variablene, så du kan bruke formelen til å beregne korrelasjonskoeffisienten. Husk at "n" er antall verdipar for begge variablene. Andre verdier er beregnet tidligere. - I vårt eksempel vil beregningene bli skrevet slik:
[
]
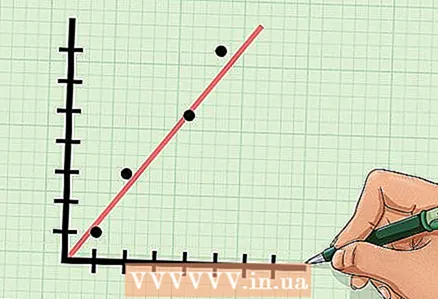 8 Analyser resultatet. I vårt eksempel er korrelasjonskoeffisienten 0,988. Denne verdien karakteriserer på en eller annen måte et gitt sett med tallpar. Vær oppmerksom på tegnet og størrelsen på verdien.
8 Analyser resultatet. I vårt eksempel er korrelasjonskoeffisienten 0,988. Denne verdien karakteriserer på en eller annen måte et gitt sett med tallpar. Vær oppmerksom på tegnet og størrelsen på verdien. - Siden verdien av korrelasjonskoeffisienten er positiv, er det en positiv korrelasjon mellom variablene "x" og "y". Det vil si at når verdien av "x" øker, øker også verdien av "y".
- Siden verdien av korrelasjonskoeffisienten er veldig nær +1, er verdiene til variablene "x" og "y" sterkt korrelert. Hvis du legger poeng på koordinatplanet, vil de være plassert nær en rett linje.
Metode 2 av 4: Bruke online kalkulatorer til å beregne korrelasjonskoeffisienten
 1 Finn en kalkulator på Internett for å beregne korrelasjonskoeffisienten. Denne koeffisienten er ofte beregnet i statistikk. Hvis det er mange tallpar, er det nesten umulig å beregne korrelasjonskoeffisienten manuelt. Derfor er det online kalkulatorer for å beregne korrelasjonskoeffisienten. I en søkemotor skriver du inn "korrelasjonskoeffisientkalkulator" (uten anførselstegn).
1 Finn en kalkulator på Internett for å beregne korrelasjonskoeffisienten. Denne koeffisienten er ofte beregnet i statistikk. Hvis det er mange tallpar, er det nesten umulig å beregne korrelasjonskoeffisienten manuelt. Derfor er det online kalkulatorer for å beregne korrelasjonskoeffisienten. I en søkemotor skriver du inn "korrelasjonskoeffisientkalkulator" (uten anførselstegn). 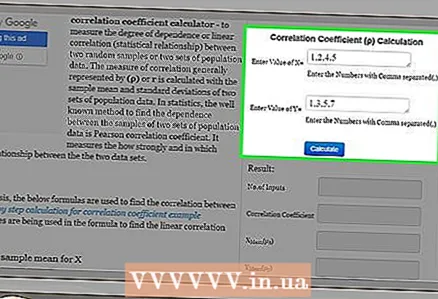 2 Skriv inn data. Sjekk instruksjonene på nettstedet for å angi riktige data (tallpar). Det er viktig å skrive inn de riktige tallparene; Ellers får du feil resultat. Husk at forskjellige nettsteder har forskjellige inndataformater.
2 Skriv inn data. Sjekk instruksjonene på nettstedet for å angi riktige data (tallpar). Det er viktig å skrive inn de riktige tallparene; Ellers får du feil resultat. Husk at forskjellige nettsteder har forskjellige inndataformater. - For eksempel, på http://ncalculators.com/statistics/correlation-coefficient-calculator.htm, angis verdiene til variablene x og y i to horisontale linjer. Verdiene skilles med komma. Det vil si at i vårt eksempel er verdiene "x" angitt slik: 1,2,4,5, og verdiene "y" slik: 1,3,5,7.
- På et annet nettsted, http://www.alcula.com/calculators/statistics/correlation-coefficient/, angis data vertikalt; i dette tilfellet må du ikke forvirre de tilsvarende parene med tall.
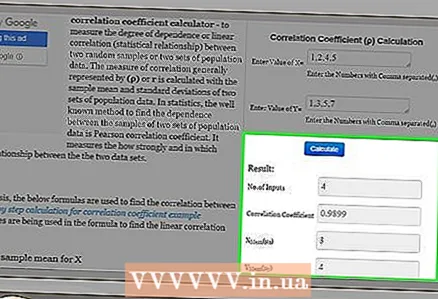 3 Beregn korrelasjonskoeffisienten. Etter å ha lagt inn dataene, klikker du bare på "Beregn", "Beregn" eller lignende knapp for å få resultatet.
3 Beregn korrelasjonskoeffisienten. Etter å ha lagt inn dataene, klikker du bare på "Beregn", "Beregn" eller lignende knapp for å få resultatet.
Metode 3 av 4: Bruke en grafisk kalkulator
 1 Skriv inn data. Ta en grafisk kalkulator, gå inn i statistisk beregningsmodus og velg kommandoen "Rediger".
1 Skriv inn data. Ta en grafisk kalkulator, gå inn i statistisk beregningsmodus og velg kommandoen "Rediger". - Ulike kalkulatorer krever at forskjellige taster trykkes. Denne artikkelen diskuterer Texas Instruments TI-86-kalkulatoren.
- Trykk på [2.] - Stat (over + -tasten) for å gå inn i den statistiske beregningsmodusen. Trykk deretter på F2 - Rediger.
 2 Slett de tidligere lagrede dataene. De fleste kalkulatorer beholder statistikken du skriver inn til du sletter dem. For å unngå å forveksle gamle data med nye, må du først slette lagret informasjon.
2 Slett de tidligere lagrede dataene. De fleste kalkulatorer beholder statistikken du skriver inn til du sletter dem. For å unngå å forveksle gamle data med nye, må du først slette lagret informasjon. - Bruk piltastene til å flytte markøren og markere overskriften 'xStat'. Trykk deretter på Slett og Enter for å slette alle verdiene som er angitt i xStat -kolonnen.
- Bruk piltastene til å markere overskriften 'yStat'. Trykk deretter på Slett og Enter for å slette alle verdiene som er angitt i yStat -kolonnen.
 3 Skriv inn de første dataene. Bruk piltastene til å flytte markøren til den første cellen under overskriften "xStat". Skriv inn den første verdien og trykk Enter. Nederst på skjermen vises “xStat (1) = __”, og den angitte verdien erstatter et mellomrom. Etter at du trykker Enter, vil den angitte verdien vises i tabellen, og markøren vil gå til neste linje; dette vil vise "xStat (2) = __" nederst på skjermen.
3 Skriv inn de første dataene. Bruk piltastene til å flytte markøren til den første cellen under overskriften "xStat". Skriv inn den første verdien og trykk Enter. Nederst på skjermen vises “xStat (1) = __”, og den angitte verdien erstatter et mellomrom. Etter at du trykker Enter, vil den angitte verdien vises i tabellen, og markøren vil gå til neste linje; dette vil vise "xStat (2) = __" nederst på skjermen. - Skriv inn alle verdiene for variabelen "x".
- Etter å ha angitt alle verdiene for x, bruker du piltastene til å navigere til yStat -kolonnen og angi verdiene for y.
- Etter å ha angitt alle tallpar, trykker du på Avslutt for å fjerne skjermen og gå ut av aggregeringsmodus.
 4 Beregn korrelasjonskoeffisienten. Det karakteriserer hvor nær dataene er til en bestemt rett linje. Grafkalkulatoren kan raskt bestemme den rette rette linjen og beregne korrelasjonskoeffisienten.
4 Beregn korrelasjonskoeffisienten. Det karakteriserer hvor nær dataene er til en bestemt rett linje. Grafkalkulatoren kan raskt bestemme den rette rette linjen og beregne korrelasjonskoeffisienten. - Klikk på Stat - Calc. Trykk på [2nd] - [Stat] - [F1] på TI -86.
- Velg funksjonen Lineær regresjon. Trykk på [F3] på TI-86 som er merket "LinR". Skjermen viser linjen "LinR _" med en blinkende markør.
- Skriv inn navnene på to variabler: xStat og yStat.
- Åpne listen over navn på TI-86; For å gjøre dette, trykk [2.] - [Liste] - [F3].
- De tilgjengelige variablene vises på bunnlinjen på skjermen. Velg [xStat] (du må sannsynligvis trykke F1 eller F2 for å gjøre dette), skriv inn et komma, og velg deretter [yStat].
- Trykk Enter for å behandle de angitte dataene.
 5 Analyser resultatene dine. Ved å trykke Enter vil skjermen vise følgende informasjon:
5 Analyser resultatene dine. Ved å trykke Enter vil skjermen vise følgende informasjon: : dette er funksjonen som beskriver linjen. Vær oppmerksom på at funksjonen ikke er skrevet i standardform (y = kx + b).
... Dette er y-koordinaten for skjæringspunktet mellom den rette linjen og y-aksen.
... Dette er skråningen på linjen.
... Dette er korrelasjonskoeffisienten.
... Dette er antall tallpar som ble brukt i beregningene.
Metode 4 av 4: Forklaring av grunnleggende begreper
 1 Forstå begrepet korrelasjon. Korrelasjon er det statistiske forholdet mellom to størrelser. Korrelasjonskoeffisienten er en numerisk verdi som kan beregnes for to datasett. Verdien av korrelasjonskoeffisienten ligger alltid i området fra -1 til +1 og karakteriserer graden av sammenheng mellom to variabler.
1 Forstå begrepet korrelasjon. Korrelasjon er det statistiske forholdet mellom to størrelser. Korrelasjonskoeffisienten er en numerisk verdi som kan beregnes for to datasett. Verdien av korrelasjonskoeffisienten ligger alltid i området fra -1 til +1 og karakteriserer graden av sammenheng mellom to variabler. - For eksempel gitt høyden og alderen på barn (ca 12 år). Mest sannsynlig vil det være en sterk positiv korrelasjon, fordi barn blir høyere med alderen.
- Et eksempel på en negativ korrelasjon: straffesekunder og tid brukt på skiskytingstrening, det vil si at jo mer en idrettsutøver trener, desto færre straffesekunder vil bli tildelt.
- Til slutt er det noen ganger veldig liten korrelasjon (positiv eller negativ), for eksempel mellom skostørrelse og matematiske poengsummer.
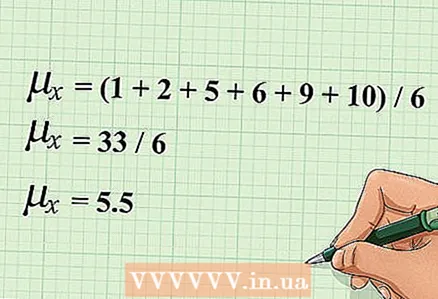 2 Husk hvordan du beregner det aritmetiske gjennomsnittet. For å beregne det aritmetiske gjennomsnittet (eller gjennomsnittet) må du finne summen av alle disse verdiene, og deretter dele det med antall verdier. Husk at det aritmetiske gjennomsnittet er nødvendig for å beregne korrelasjonskoeffisienten.
2 Husk hvordan du beregner det aritmetiske gjennomsnittet. For å beregne det aritmetiske gjennomsnittet (eller gjennomsnittet) må du finne summen av alle disse verdiene, og deretter dele det med antall verdier. Husk at det aritmetiske gjennomsnittet er nødvendig for å beregne korrelasjonskoeffisienten. - Gjennomsnittsverdien til en variabel er angitt med en bokstav med en horisontal stolpe over den. For eksempel, når det gjelder variablene "x" og "y", er gjennomsnittsverdiene deres angitt som følger: x̅ og y̅. Gjennomsnittet er noen ganger betegnet med den greske bokstaven "μ" (mu). For å skrive det aritmetiske gjennomsnittet av verdiene til variabelen "x", bruker du notasjonen μx eller μ (x).
- For eksempel gitt følgende verdier for variabelen "x": 1,2,5,6,9,10. Det aritmetiske gjennomsnittet av disse verdiene beregnes som følger:
 3 Legg merke til viktigheten av standardavviket. I statistikk karakteriserer standardavviket i hvilken grad tall er spredt i forhold til gjennomsnittet. Hvis standardavviket er lite, er tallene nær gjennomsnittet; hvis standardavviket er stort, er tallene langt fra gjennomsnittet.
3 Legg merke til viktigheten av standardavviket. I statistikk karakteriserer standardavviket i hvilken grad tall er spredt i forhold til gjennomsnittet. Hvis standardavviket er lite, er tallene nær gjennomsnittet; hvis standardavviket er stort, er tallene langt fra gjennomsnittet. - Standardavvik er angitt med bokstaven "s" eller den greske bokstaven "σ" (sigma). Dermed er standardavviket for verdiene til variabelen "x" betegnet som følger: sx eller σx.
 4 Husk symbolet for summeringsoperasjonen. Summasjonssymbolet er et av de vanligste symbolene i matematikk og angir summen av verdier. Dette symbolet er den greske bokstaven "Σ" (store bokstaver).
4 Husk symbolet for summeringsoperasjonen. Summasjonssymbolet er et av de vanligste symbolene i matematikk og angir summen av verdier. Dette symbolet er den greske bokstaven "Σ" (store bokstaver). - For eksempel, hvis gitt følgende verdier for variabelen "x": 1,2,5,6,9,10, betyr Σx:
- 1 + 2 + 5 + 6 + 9 + 10 = 33.
- For eksempel, hvis gitt følgende verdier for variabelen "x": 1,2,5,6,9,10, betyr Σx:
Tips
- Korrelasjonskoeffisienten kalles noen ganger "Pearson -korrelasjonskoeffisienten" etter utvikleren Carl Pearson.
- I de fleste tilfeller, når korrelasjonskoeffisienten er større enn 0,8 (positiv eller negativ), er det en sterk korrelasjon; hvis korrelasjonskoeffisienten er mindre enn 0,5 (positiv eller negativ), observeres en svak korrelasjon.
Advarsler
- Korrelasjon kjennetegner forholdet mellom verdiene til to variabler. Men husk at korrelasjon ikke har noe å gjøre med årsakssammenheng. For eksempel, hvis du sammenligner høyden og skostørrelsen til mennesker, vil du sannsynligvis finne en sterk positiv sammenheng. Vanligvis, jo høyere personen er, desto større er skostørrelsen. Men dette betyr ikke at en økning i høyden fører til en automatisk økning i skostørrelse, eller at større føtter vil føre til raskere vekst. Disse mengdene henger rett og slett sammen.



