Innhold

• Trinn
• Del 1 av 3: Enkelhetstester
• Del 2 av 3: Hvordan enkelhetstester fungerer
• Del 3 av 3: Bruke den kinesiske restteoremet
• Tips
• Hva trenger du

Primtall er tall som bare kan deles av seg selv og med 1. Alle andre tall kalles sammensatte tall. Det er mange måter å avgjøre om et tall er primtall, og de har alle sine egne fordeler og ulemper. På den ene siden er noen av metodene veldig nøyaktige, men de er ganske komplekse hvis du har å gjøre med store tall. På den annen side er det mye raskere måter, men de kan føre til feil resultater. Valget av riktig metode avhenger av hvor store tall du jobber med.

Trinn

Del 1 av 3: Enkelhetstester

Merk: i alle formler n angir nummeret som skal kontrolleres.

1. 1 Opptelling av delere. Det er nok å dele n til alle primtall fra 2 til den avrundede verdien (${ displaystyle { sqrt {n}}}$).
2. 2 Fermats lille teorem. Advarsel: Noen ganger vil testen feilaktig identifisere sammensatte tall som primtall, selv for alle verdier av a.
   • La oss velge et helt tall enslik at 2 ≤ a ≤ n - 1.
   • Hvis a (mod n) = a (mod n) er tallet sannsynligvis primtall. Hvis likheten ikke er tilfredsstilt, er tallet n sammensatt.
   • Sjekk gitt likhet for flere verdier enfor å øke sannsynligheten for at antallet som testes faktisk er førsteklasses.
3. 3 Miller-Rabin-test. Advarsel: Noen ganger, men sjelden, for flere verdier av a, vil testen feilaktig identifisere sammensatte tall som primtall.
   • Finn mengdene s og d slik at ${ displaystyle n-1 = 2 ^ {s} * d}$.
   • Velg et heltall en i området 2 ≤ a ≤ n - 1.
   • Hvis a = +1 (mod n) eller -1 (mod n), er n sannsynligvis primtall. I dette tilfellet, gå til testresultatet. Hvis likestillingen ikke holder, gå til neste trinn.
   • Firkant svaret ditt (${ displaystyle a ^ {2d}}$). Hvis du får -1 (mod n), er n sannsynligvis et primtall. I dette tilfellet, gå til testresultatet. Hvis likheten mislykkes, gjenta (${ displaystyle a ^ {4d}}$ og så videre) til ${ displaystyle a ^ {2 ^ {s-1} d}}$.
   • Hvis du på et eller annet trinn etter kvadrering av et annet tall enn ${ displaystyle pm 1}$ (mod n), du har +1 (mod n), så n er et sammensatt tall. Hvis ${ displaystyle a ^ {2 ^ {s-1} d} neq pm 1}$ (mod n), så er n ikke prime.
   • Testresultat: hvis n består testen, gjenta den for andre verdier enå øke tilliten.

Del 2 av 3: Hvordan enkelhetstester fungerer

1. 1 Opptelling av delere. Per definisjon, tallet n er enkelt bare hvis det ikke er delbart med 2 og andre heltall unntatt 1 og seg selv. Formelen ovenfor lar deg fjerne unødvendige trinn og spare tid: for eksempel, etter å ha sjekket om et tall er delbart med 3, er det ikke nødvendig å sjekke om det er delbart med 9.
   • Gulvfunksjonen (x) avrunder x til nærmeste heltall mindre enn eller lik x.
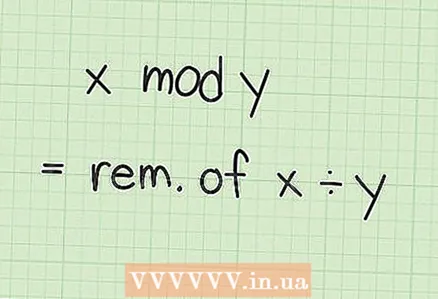2. 2 Lær om modulær regning. Operasjonen "x mod y" (mod er en forkortelse av det latinske ordet "modulo", det vil si "modul") betyr "dele x med y og finne resten." Med andre ord, i modulær aritmetikk, når du når en viss verdi, som kalles modul, tallene "går" til null igjen. For eksempel teller klokken ned med modul 12: den viser 10, 11 og 12 timer, og går deretter tilbake til 1.
   • Mange kalkulatorer har en mod -nøkkel. Slutten av denne delen viser deg hvordan du manuelt beregner denne funksjonen for store tall.
3. 3 Lær om fallgruvene til Fermats lille teorem. Alle tall som testbetingelsene ikke er oppfylt for, er sammensatte, men resten av tallene er bare sannsynligvis er enkle. Hvis du vil unngå feil resultater, søker du n i listen over "Carmichael -tall" (sammensatte tall som tilfredsstiller denne testen) og "Fermat -pseudoprime -tall" (disse tallene oppfyller testbetingelsene bare for noen verdier en).
4. 4 Hvis det er praktisk, bruk Miller-Rabin-testen. Selv om denne metoden er ganske tungvint for manuelle beregninger, brukes den ofte i dataprogrammer. Det gir akseptabel hastighet og færre feil enn Fermats metode. Et sammensatt tall vil ikke bli tatt som et primtall hvis beregninger utføres for mer enn ¼ verdier en... Hvis du tilfeldig velger forskjellige verdier en og for dem alle vil testen gi et positivt resultat, det kan vi anta med ganske høy grad av tillit til n er et primtall.
5. 5 For store tall, bruk modulær aritmetikk. Hvis du ikke har en modkalkulator for hånden, eller hvis kalkulatoren ikke er designet for å håndtere så store tall, bruker du strømegenskaper og modulregning for å gjøre beregningene enklere. Nedenfor er et eksempel på ${ displaystyle 3 ^ {50}}$ mod 50:
   • Skriv om uttrykket i en mer praktisk form: ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50. Manuelle beregninger kan kreve ytterligere forenklinger.
   • ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50 = ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50. Her tok vi hensyn til egenskapen til modulær multiplikasjon.
   • ${ displaystyle 3 ^ {25}}$ mod 50 = 43.
   • ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50 = ${ displaystyle (43 * 43)}$ mod 50.
   • ${ displaystyle = 1849}$ mod 50.
   • ${ displaystyle = 49}$.

Del 3 av 3: Bruke den kinesiske restteoremet

1. 1 Velg to tall. Ett av tallene må være sammensatt, og det andre må være nøyaktig det du vil teste for enkelhet.
   • Nummer 1 = 35
   • Nummer 2 = 97
2. 2 Velg to verdier som er større enn null og henholdsvis mindre enn tallene Number1 og Number2. Disse verdiene må ikke være de samme.
   • Verdi1 = 1
   • Verdi2 = 2
3. 3 Beregn MMI (Mathematical Multiplicative Inverse) for Number1 og Number2.
   • Beregn MMI
     • MMI1 = Number2 ^ -1 Mod Number1
     • MMI2 = Number1 ^ -1 Mod Number2
   • Bare for primtall (dette vil gi et tall for sammensatte tall, men det vil ikke være hans MMI):
     • MMI1 = (Number2 ^ (Number1-2))% Number1
     • MMI2 = (Number1 ^ (Number2-2))% Number2
   • For eksempel:
     • MMI1 = (97 ^ 33)% 35
     • MMI2 = (35 ^ 95)% 97
4. 4 Lag en tabell for hver MMI ned til log2 moduler:
   • For MMI1
     • F (1) = Antall2% Antall1 = 97% 35 = 27
     • F (2) = F (1) * F (1)% Antall1 = 27 * 27% 35 = 29
     • F (4) = F (2) * F (2)% Antall1 = 29 * 29% 35 = 1
     • F (8) = F (4) * F (4)% Antall1 = 1 * 1% 35 = 1
     • F (16) = F (8) * F (8)% Antall1 = 1 * 1% 35 = 1
     • F (32) = F (16) * F (16)% Antall1 = 1 * 1% 35 = 1
   • Beregn sammenkoblede tall 1 - 2
     • 35 -2 = 33 (10001) base 2
     • MMI1 = F (33) = F (32) * F (1) mod 35
     • MMI1 = F (33) = 1 * 27 mod 35
     • MMI1 = 27
   • For MMI2
     • F (1) = Antall1% Antall2 = 35% 97 = 35
     • F (2) = F (1) * F (1)% Antall2 = 35 * 35 mod 97 = 61
     • F (4) = F (2) * F (2)% Antall2 = 61 * 61 mod 97 = 35
     • F (8) = F (4) * F (4)% Antall2 = 35 * 35 mod 97 = 61
     • F (16) = F (8) * F (8)% Antall2 = 61 * 61 mod 97 = 35
     • F (32) = F (16) * F (16)% Antall2 = 35 * 35 mod 97 = 61
     • F (64) = F (32) * F (32)% Antall2 = 61 * 61 mod 97 = 35
     • F (128) = F (64) * F (64)% Antall2 = 35 * 35 mod 97 = 61
   • Beregn paret nummer 2 - 2
     • 97 - 2 = 95 = (1011111) base 2
     • MMI2 = (((((F (64) * F (16)% 97) * F (8)% 97) * F (4)% 97) * F (2)% 97) * F) (1)% 97)
     • MMI2 = (((((35 * 35)% 97) * 61)% 97) * 35% 97) * 61% 97) * 35% 97)
     • MMI2 = 61
5. 5 Beregn (verdi1 * tall2 * MMI1 + verdi2 * tall1 * MMI2)% (tall1 * tall2)
   • Svar = (1 * 97 * 27 + 2 * 35 * 61)% (97 * 35)
   • Svar = (2619 + 4270)% 3395
   • Svar = 99
6. 6 Kontroller at Number1 ikke er prime
   • Beregn (svar - verdi1)% tall1
   • 99 – 1 % 35 = 28
   • Siden 28 er større enn 0, er 35 ikke et primtall.
7. 7 Sjekk at Number2 er prime.
   • Beregn (svar - verdi2)% tall2
   • 99 – 2 % 97 = 0
   • Siden 0 er 0, er 97 mest sannsynlig et primtall.
8. 8 Gjenta trinn 1 til 7 minst to ganger til.
   • Hvis du får 0 i trinn 7:
     • Bruk et annet tall1 hvis tall1 ikke er primtall.
     • Bruk et annet tall1 hvis tall1 er primtall. I dette tilfellet bør du få 0 i trinn 6 og 7.
     • Bruk forskjellig mening1 og mening2.
   • Hvis du i trinn 7 konsekvent får 0, er det sannsynlig at nummer 2 er primtall.
   • Trinn 1 til og med 7 kan resultere i en feil hvis Number1 ikke er prime og Number2 er en divisor av Number1. Den beskrevne metoden fungerer i alle tilfeller når begge tallene er primtall.
   • Grunnen til at du trenger å gjenta trinn 1 til 7 er fordi i noen tilfeller, selv om nummer 1 og nummer 2 ikke er primtall, får du i trinn 7 0 (for ett eller begge tallene). Dette skjer sjelden.Velg et annet tall1 (sammensatt), og hvis tall2 ikke er primtall, vil ikke tall2 være lik null i trinn 7 (bortsett fra tilfellet når tall1 er en divisor for tall2 - her vil primtalene alltid være lik null i trinn 7).

Tips

• Primtall fra 168 til 1000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
• Selv om brute force testing er en kjedelig test når du arbeider med store tall, er det ganske effektivt for små tall. Selv når det gjelder store tall, begynn med å teste små divisorer, og fortsett deretter til mer sofistikerte metoder for å kontrollere enkelheten i tall (hvis det ikke finnes små divisorer).

Hva trenger du

• Papir, penn eller datamaskin