Innhold

• Trinn
• Tips

Den rasjonelle funksjonen har formen y = N (x) / D (x), hvor N og D er polynomer. For å plotte en slik funksjon nøyaktig trenger du god kunnskap om algebra, inkludert differensialberegninger. Vurder følgende eksempel: y = (2x - 6x + 5)/(4x + 2).

Trinn

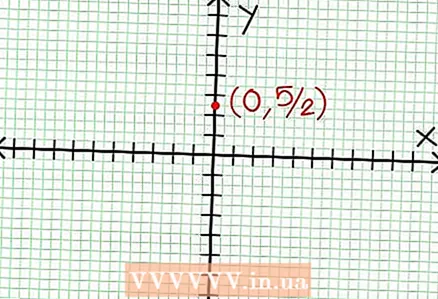1. 1 Finn y-skjæringen i grafen. For å gjøre dette, erstatt x = 0 i funksjonen og få y = 5/2. Dermed har skjæringspunktet mellom grafen og Y -aksen koordinater (0, 5/2).Plasser dette punktet på koordinatplanet.
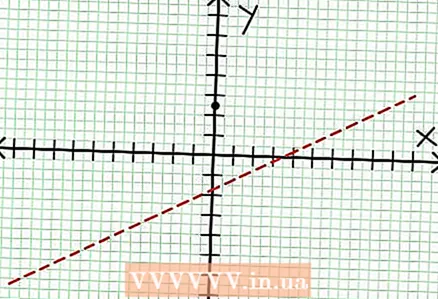2. 2 Finn de horisontale asymptotene. Del telleren med nevneren (i en kolonne) for å bestemme oppførselen til "y" med verdier på "x" som har en tendens til uendelig. I vårt eksempel vil divisjonen være y = (1/2)x - (7/4) + 17/(8x + 4). For store positive eller negative verdier på "x" 17 / (8x + 4) har en tendens til null, og grafen nærmer seg den rette linjen gitt av funksjonen y = (1/2)x - (7/4). Plott denne funksjonen ved hjelp av den stiplede linjen.
   • Hvis tellergraden er mindre enn nevneren, kan du ikke dele telleren med nevneren, og asymptoten vil bli beskrevet av funksjonen på = 0.
   • Hvis tellergraden er lik nevnergraden, er asymptoten en horisontal linje lik forholdet mellom koeffisientene ved "x" i høyeste grad.
   • Hvis tellerens grad er 1 mer enn nevnergraden, er asymptoten en skrå rett linje, hvis helling er lik forholdet mellom koeffisientene ved "x" til den høyeste grad.
   • Hvis tellerens grad er større enn nevneren med 2, 3, etc., så for store verdier |NS| betydning på har en tendens til uendelig (positiv eller negativ) i form av en firkant, kubikk eller annen grad av et polynom. I dette tilfellet trenger du sannsynligvis ikke å lage en eksakt graf over funksjonen som oppnås ved å dele telleren med nevneren.
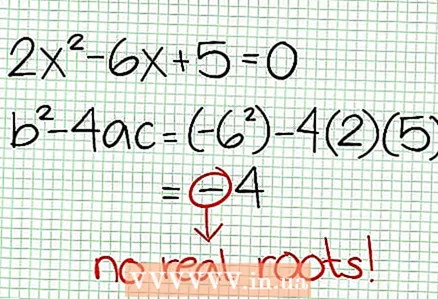3. 3 Finn nullene til funksjonen. En rasjonell funksjon har nuller når telleren er null, det vil si N (NS) = 0. I vårt eksempel, 2x - 6x + 5 = 0. Diskriminanten av denne kvadratiske ligningen: b - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Siden diskriminanten er negativ, så er N (NS), og dermed F (NS) har ingen virkelige røtter. Grafen til en rasjonell funksjon skjærer ikke X-aksen. Hvis funksjonen har nuller (røtter), legg dem på koordinatplanet.
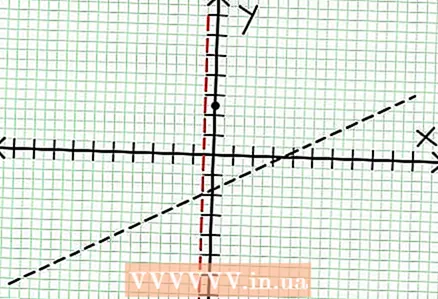4. 4 Finn de vertikale asymptotene. For å gjøre dette, sett nevneren til null. I vårt eksempel, 4x + 2 = 0 og NS = -1/2. Plott den vertikale asymptoten ved hjelp av den stiplede linjen. Hvis for noen verdi NS N (NS) = 0 og D (NS) = 0, så eksisterer den vertikale asymptoten enten eller eksisterer ikke (dette er et sjeldent tilfelle, men det er bedre å huske det).
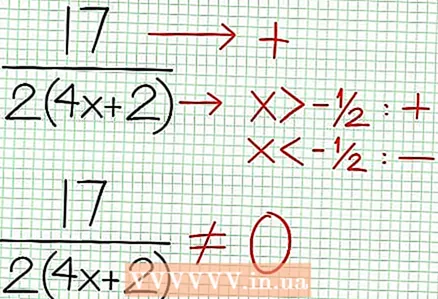5. 5 Se på resten av telleren dividert med nevneren. Er det positivt, negativt eller null? I vårt eksempel er resten 17, noe som er positivt. Nevner 4x + 2 positive til høyre for den vertikale asymptoten og negative til venstre for den. Dette betyr at grafen for den rasjonelle funksjonen for store positive verdier NS nærmer seg asymptoten ovenfra, og for store negative verdier NS - nedenfra. Siden 17 / (8x + 4) er aldri lik null, da vil grafen for denne funksjonen aldri skjære den rette linjen spesifisert av funksjonen på = (1/2)NS - (7/4).
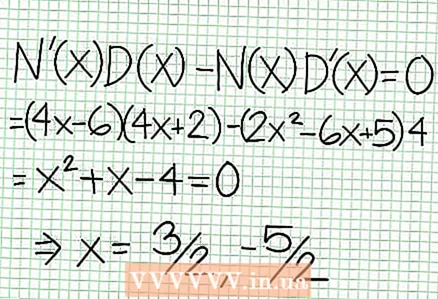6. 6 Finn lokalt ekstrema. Det finnes et lokalt ekstremum for N '(x) D (x) - N (x) D ’(x) = 0. I vårt eksempel er N ’(x) = 4x - 6 og D '(x) = 4. N ’(x) D (x) - N (x) D ’(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Når du løser denne ligningen, finner du det x = 3/2 og x = -5/2. (Dette er ikke helt nøyaktige verdier, men de passer for vårt tilfelle når det ikke er behov for overpresisjon.)
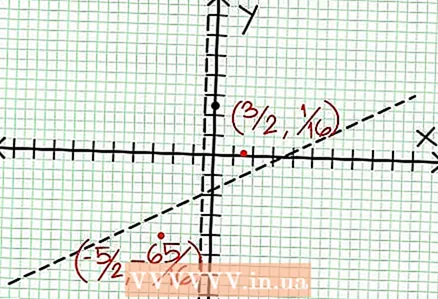7. 7 Finn verdien på for hver lokal ekstremum. For å gjøre dette, erstatt verdiene NS inn i den opprinnelige rasjonelle funksjonen. I vårt eksempel er f (3/2) = 1/16 og f (-5/2) = -65/16. Sett av punkter (3/2, 1/16) og (-5/2, -65/16) på koordinatplanet. Siden beregningene er basert på omtrentlige verdier (fra forrige trinn), er minimum og maksimum funnet heller ikke helt nøyaktig (men sannsynligvis veldig nær de eksakte verdiene). (Punktet (3/2, 1/16) er veldig nær det lokale minimumet. Fra trinn 3 vet vi det på alltid positiv for NS> -1/2, og vi fant en liten verdi (1/16); dermed er feilverdien ekstremt liten i dette tilfellet.)
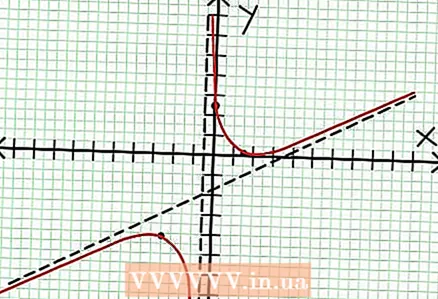8. 8 Koble de ventende punktene og utvid grafen jevnt til asymptotene (ikke glem den riktige retningen til grafen som nærmer seg asymptotene). Husk at grafen ikke må krysse X-aksen (se trinn 3). Grafen skjærer heller ikke de horisontale og vertikale asymptotene (se trinn 5). Ikke endre retningen på diagrammet bortsett fra på de ekstreme punktene som ble funnet i forrige trinn.

Tips

• Hvis du fulgte trinnene ovenfor strengt i rekkefølge, er det ikke nødvendig å beregne andre derivater (eller lignende komplekse mengder) for å teste løsningen.
• Hvis du ikke trenger å beregne verdiene av mengder, kan du erstatte å finne lokalt ekstrema ved å beregne noen ekstra par koordinater (NS, på) mellom hvert par asymptoter. Dessuten, hvis du ikke bryr deg om hvordan den beskrevne metoden fungerer, så ikke bli overrasket over hvorfor du ikke kan finne derivatet og løse ligningen N '(x) D (x) - N (x) D ’(x) = 0.
• I noen tilfeller må du jobbe med polynom av høyere orden. Hvis du ikke finner den eksakte løsningen ved hjelp av faktorisering, formler, etc., kan du estimere mulige løsninger ved hjelp av numeriske metoder som Newtons metode.
• I sjeldne tilfeller har teller og nevner en felles variabel faktor. I henhold til trinnene beskrevet vil dette føre til null og en vertikal asymptote på samme sted. Dette er imidlertid ikke mulig, og forklaringen er en av følgende:
  • Null i N (NS) har en høyere multiplisitet enn null i D (NS). Graf F (NS) har en tendens til null på dette punktet, men er ikke definert der. Angi dette ved å tegne en sirkel rundt punktet.
  • Null i N (NS) og null i D (NS) har samme mangfold. Grafen nærmer seg et ikke-nullpunkt ved denne verdien NSmen ikke definert der. Angi dette ved å tegne en sirkel rundt punktet.
  • Null i N (NS) har en lavere multiplisitet enn null i D (NS). Det er en vertikal asymptote her.