Innhold

• Fremgangsmåte
• Råd

I motsetning til en rett linje endres koeffisienten for skråningen (skråningen) kontinuerlig når den beveger seg langs kurven. Calculus gir ideen om at hvert punkt i grafen kan uttrykkes som en vinkelkoeffisient eller "øyeblikkelig endringshastighet". Tangenslinjen ved et punkt er en linje som har samme vinkelkoeffisient og går gjennom samme punkt. For å finne en tangentlinjeligning, må du vite hvordan du kan utlede den opprinnelige ligningen.

Fremgangsmåte

Metode 1 av 2: Finn ligningen for tangentlinjen

1. 

   Graffunksjoner og tangentlinjer (dette trinnet er valgfritt, men anbefales). Diagrammet vil hjelpe deg lettere å forstå problemet og sjekke om svaret er rimelig eller ikke. Tegn funksjonelle grafer på rutenettpapir, bruk den vitenskapelige kalkulatoren med graffunksjon for referanse hvis nødvendig. Tegn en tangentlinje gjennom et gitt punkt (Husk at tangentlinjen passerer gjennom det punktet og har samme skråning som grafen der).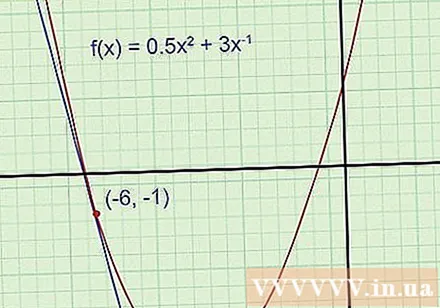
   • Eksempel 1: Tegn parabolsk. Tegn en tangenslinje gjennom punktet (-6, -1).
     Selv om du ikke kjenner tangentligningen, kan du fremdeles se at skråningen er negativ og skjæringspunktet er negativt (langt under parabolske toppunkt med ordinaten -5,5). Hvis det endelige svaret som er funnet ikke samsvarer med disse detaljene, må det være en feil i beregningen din, og du må sjekke igjen.

2. 

   
   
   Få det første derivatet som finner ligningen skråningen av tangentlinjen. Med funksjonen f (x) representerer det første derivatet f '(x) ligningen for hellingen til tangentlinjen på et hvilket som helst punkt på f (x). Det er mange måter å ta derivater på. Her er et enkelt eksempel som bruker strømregelen:
   • Eksempel 1 (forts.): Grafen er gitt av en funksjon.
     Tilbakekalle kraftregelen når du tar derivater:.
     Det første derivatet av funksjonen = f '(x) = (2) (0,5) x + 3 - 0.
     f '(x) = x + 3. Ved å erstatte x med en hvilken som helst verdi a, vil ligningen gi oss hellingen til tangensfunksjonen f (x) i punkt x = a.

3. 

   
   
   Angi x-verdien til det aktuelle punktet. Les problemet for å finne koordinatene til punktet for å finne tangenslinjen. Skriv inn koordinaten til dette punktet i f '(x). Det oppnådde resultatet er hellingen til tangentlinjen ved punktet ovenfor.
   • Eksempel 1 (forts.): Poenget nevnt i artikkelen er (-6, -1). Ved å bruke diagonal -6 spenning til f '(x):
     f '(- 6) = -6 + 3 = -3
     Tangenslinjens skråning er -3.

4. 

   
   
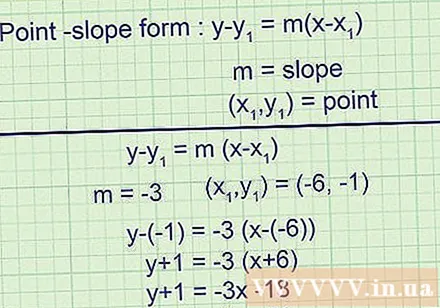
   Skriv en ligning for en tangentlinje med formen av en rett linje og kjenn koeffisienten til vinkelen og et punkt på den. Denne lineære ligningen er skrevet som. Innsiden, m er skråningen og er et punkt på tangentlinjen. Du har nå all informasjonen du trenger for å skrive en tangentligning i dette skjemaet.
   • Eksempel 1 (forts.):
     Tangenslinjens skråning er -3, så:
     Tangentlinjen passerer gjennom punktet (-6, -1), så den endelige ligningen er:
     Kort sagt kan vi:
     

5. 

   Grafisk bekreftelse. Hvis du har en grafkalkulator, kan du tegne den opprinnelige funksjonen og tangentlinjen for å sjekke om svaret er riktig. Hvis du gjør beregninger på papir, kan du bruke grafer tegnet tidligere for å sikre at det ikke er noen åpenbare feil i svaret ditt.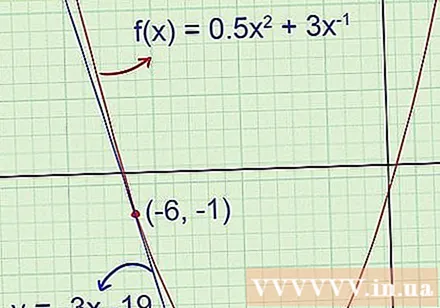
   • Eksempel 1 (forts.): Den innledende tegningen viser at tangentlinjen har negative vinkelkoeffisienter og forskyvningen er langt under -5,5. Tangensligningen som nettopp er funnet er y = -3x -19, noe som betyr at -3 er skråningen av vinkelen og -19 er ordinaten.

6. 

   Prøv å løse et vanskeligere problem. Vi går gjennom alle trinnene ovenfor igjen.På dette punktet er målet å finne tangentlinjen til at x = 2: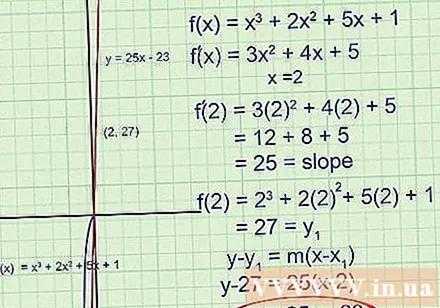
   • Finn det første derivatet ved hjelp av kraftregelen :. Denne funksjonen vil gi oss tangentens skråning.
   • For x = 2, finn. Dette er skråningen ved x = 2.
   • Merk at denne gangen har vi ikke et poeng og bare x-koordinaten. For å finne y-koordinaten, erstatt x = 2 i den opprinnelige funksjonen :. Poengsummen er (2.27).
   • Skriv en ligning for en tangentlinje som går gjennom et punkt og har koeffisienten til vinkelen bestemt:
     
     Reduser om nødvendig til y = 25x - 23.
   annonse

Metode 2 av 2: Løs relaterte problemer

1. 

   Finn det ekstreme på grafen. De er punktene der grafen nærmer seg et lokalt maksimum (et poeng høyere enn nabopunktene på begge sider) eller et lokalt minimum (lavere enn nabopunktene på begge sider). Tangentlinjen har alltid en nullkoeffisient på disse punktene (en horisontal linje). Imidlertid er koeffisienten til vinkelen ikke nok til å konkludere med at det er det ekstreme punktet. Slik finner du dem: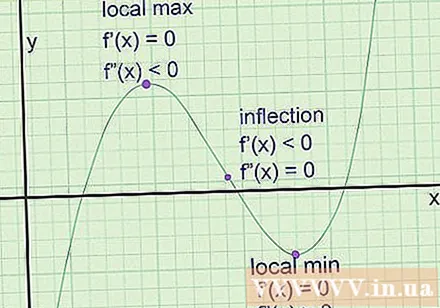
   • Ta den første avledede av funksjonen for å få f '(x), hellingen til hellingen til tangentlinjen.
   • Løs ligningen f '(x) = 0 for å finne ekstreme punkt potensiell.
   • Tar vi det kvadratiske derivatet for å få f '(x), forteller ligningen hastigheten på endring av helling av tangentlinjen.
   • Ved hvert potensielle ekstreme endrer du koordinaten en inn i f '' (x). Hvis f '(a) er positiv, har vi et lokalt minimum på en. Hvis f '(a) er negativ, har vi et lokalt maksimumspunkt. Hvis f '(a) er 0, vil det ikke være det ekstreme, det er et bøyepunkt.
   • Hvis maks eller min nådd kl en, finn f (a) for å bestemme krysset.

2. 

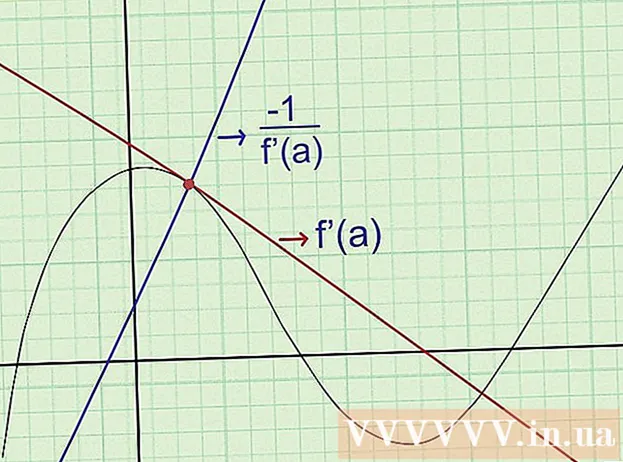
   Finn ligningene til det normale. Den "normale" linjen til en kurve ved et gitt punkt a går gjennom dette punktet og er vinkelrett på tangentlinjen. For å finne ligningen for det normale, bruk følgende: (helling av det normale) (helling av det normale) = -1 når de passerer samme punkt på grafen. Nærmere bestemt: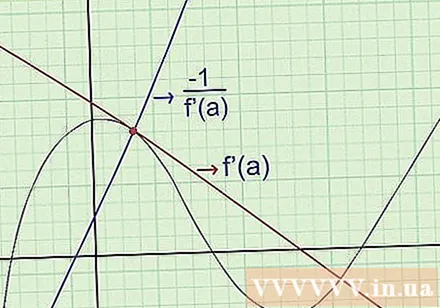
   • Finn f '(x), hellingen til tangentlinjen.
   • Hvis vi på et gitt punkt har x = en: finn f '(a) for å bestemme skråningen på det punktet.
   • Beregn for å finne koeffisienten til det normale.
   • Skriv ligningen for vinkelrett på å kjenne koeffisientene til vinkelen og et punkt den passerer gjennom.
   annonse

Råd

• Om nødvendig skriver du om den opprinnelige ligningen i standardform: f (x) = ... eller y = ...