Hvordan transponere en matrise

Innhold

Trinn
Del 1 av 3: Transpone the Matrix
Del 2 av 3: Transposisjonsegenskaper
Del 3 av 3: Hermitisk konjugatmatrise med komplekse elementer
Tips

Hvis du lærer å transponere matriser, vil du få en bedre forståelse av strukturen. Du vet kanskje allerede om firkantmatriser og deres symmetri for å hjelpe deg med å mestre transponering. Blant annet hjelper transponering med å transformere vektorer til matriseform og finne vektorprodukter. Når du arbeider med komplekse matriser, kan hermitisk-konjugerte (konjugat-transponere) matriser hjelpe deg med å løse en rekke problemer.

Trinn

Del 1 av 3: Transpone the Matrix

1 Ta en hvilken som helst matrise. Enhver matrise kan transponeres, uavhengig av antall rader og kolonner. Oftest er det nødvendig å transponere firkantede matriser som har samme antall rader og kolonner, så for enkelhets skyld bør du vurdere følgende matrise som et eksempel:
- matrisen EN =
  1  2  3
  4  5  6
  7  8  9
2 Tenk deg den første raden i en direkte matrise som den første kolonnen i den transponerte matrisen. Bare skriv den første linjen som en kolonne:
- transponert matrise = A
- første kolonne i matrise A:
  1
  2
  3
3 Gjør det samme for resten av linjene. Den andre raden i den opprinnelige matrisen blir den andre kolonnen i den transponerte matrisen. Oversett alle radene til kolonner:
- EN =
  1  4  7
  2  5  8
  3  6  9
4 Prøv å transponere en ikke-kvadratisk matrise. Enhver rektangulær matrise kan transponeres på samme måte. Bare skriv den første linjen som den første kolonnen, den andre linjen som den andre kolonnen, og så videre. I eksemplet nedenfor er hver rad i den opprinnelige matrisen merket med sin egen farge for å gjøre det tydeligere hvordan den transformeres ved transponering:
- matrisen Z =
  4 7 2 1
  3 9 8 6
- matrisen Z =
  4  3
  7  9
  2  8
  1  6
5 La oss uttrykke transposisjonen i form av en matematisk notasjon. Selv om tanken på transponering er veldig enkel, er det best å skrive den ned som en streng formel. Matrisenotasjon krever ingen spesielle vilkår:
- Anta gitt en matrise B bestående av m x n elementer (m rader og n kolonner), så er den transponerte matrisen B et sett med n x m elementer (n rader og m kolonner).
- For hvert element b_xy (linje x og kolonne y) av matrisen B i matrisen B finnes det et ekvivalent element b_yx (linje y og kolonne x).

Del 2 av 3: Transposisjonsegenskaper

1 (M. = M. Etter dobbel transponering oppnås den opprinnelige matrisen. Dette er ganske åpenbart, siden når du transponerer på nytt, endrer du radene og kolonnene igjen, noe som resulterer i den opprinnelige matrisen.
2 Speil matrisen rundt hoveddiagonalen. Kvadratiske matriser kan "vendes" i forhold til hoveddiagonalen. Videre er elementene langs hoveddiagonalen (fra a₁₁ til nedre høyre hjørne av matrisen) forblir på plass, og resten av elementene beveger seg til den andre siden av denne diagonalen og forblir i samme avstand fra den.
- Hvis du synes det er vanskelig å forestille seg denne metoden, kan du ta et stykke papir og tegne en 4x4 -matrise. Omorganiser deretter sideelementene i forhold til hoveddiagonalen. Spor samtidig elementene a₁₄ og a₄₁... Når de er transponert, må de byttes ut som andre par sideelementer.
3 Transponer den symmetriske matrisen. Elementene i en slik matrise er symmetriske om hoveddiagonalen. Hvis du gjør operasjonen ovenfor og "vender" den symmetriske matrisen, vil den ikke endres. Alle elementene endres til lignende. Faktisk er dette standardmetoden for å avgjøre om en gitt matrise er symmetrisk. Hvis likheten A = A holder, er matrisen A symmetrisk.

Del 3 av 3: Hermitisk konjugatmatrise med komplekse elementer

1 Vurder en kompleks matrise. Elementene i en kompleks matrise består av virkelige og imaginære deler. En slik matrise kan også transponeres, selv om det i de fleste praktiske applikasjoner brukes konjugat-transponert eller hermitisk-konjugatmatrise.
- La det bli gitt en matrise C =
  2+Jeg 3-2Jeg
  0+Jeg 5+0Jeg
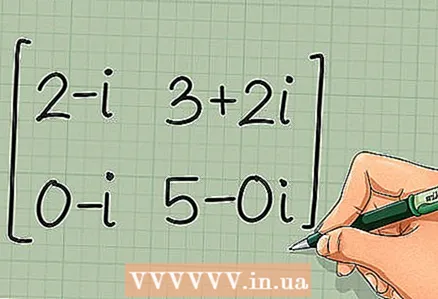2 Erstatt elementene med komplekse konjugerte tall. Ved drift av kompleks bøyning forblir den virkelige delen den samme, og den imaginære delen endrer tegnet til det motsatte. La oss gjøre dette med alle fire elementene i matrisen.
- finn den komplekse konjugerte matrisen C * =
  2-Jeg 3+2Jeg
  0-Jeg 5-0Jeg
3 Vi transponerer den resulterende matrisen. Ta den funnet komplekse konjugerte matrisen og bare transponer den. Som et resultat får vi en konjugat-transponert (hermitisk-konjugat) matrise.
- den konjugerte-transponerte matrisen C =
  2-Jeg 0-Jeg
  3+2Jeg 5-0Jeg

Tips

I denne artikkelen er den transponerte matrisen i forhold til matrisen A betegnet som A. Det er også notasjonen A 'eller Ã.
I denne artikkelen er Hermitian-konjugatmatrisen med hensyn til matrisen A betegnet som A, som er en vanlig notasjon i lineær algebra. I kvantemekanikk brukes ofte notasjonen A.Noen ganger er en hermitisk konjugatmatrise skrevet i formen A *, men det er bedre å unngå denne notasjonen, siden den også brukes til å skrive en kompleks konjugatmatrise.